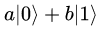I Majstrandens bostäder är det drygt 300 grader för varmt för kvantdatorn.
En av de största utmaningarna för kvantdatorerna är yttre störningar. Som vi beskrev i förra artikeln är superpositionen, där qubiten är både 0 och 1 samtidigt, oerhört känslig och kollapsar väldigt lätt. Dagens kvantdatorer fungerar vid en temperatur på ca 0.2 K, vilket är ungefär -272.95 C. Även denna rysliga kyla är lite för varmt för att uppehålla superposition. Då superpositionen kollapsar blir din qubit, som ursprungligen var både 1 och 0 samtidigt genom svart kvantmagi, en ”normal” bit med ett definitivt värde (antingen 0 eller 1) och vi förlorar information.
En simpel krets som sammanflätar två qubitar.
En längre krets.
I bilderna ovan syns två olika kretsar som kan implementeras på en kvantdator för att utföra något spännande. Operationen “H” i bilderna sätter en qubit i superposition, och för att uppehålla den så genom hela beräkningen måste vi ha en temperatur som är så nära absoluta nollpunkten som möjligt. Ju längre kretsarna är, desto mer sannolikt är det att det sker ett fel.
En annan begränsning är antalet qubitar som kvantdatorerna har i dag. Några av de större kvantdatorerna, bl.a. Googles och IBMs, har kring 50 qubitar. Även om 50 är rätt så många (för en kvantdator) så finns det beräkningar och problem som skulle kräva storleksordningar flera qubitar. En både lovande och icke-intuitiv egenskap är att en större mängd qubitar tycks hålla superpositionerna bättre.
Trots att vi inte ännu har perfekta kvantdatorer så kan vi redan göra nyttiga saker med dem. Kvantdatorer är inte bra på allt, men de saker de är bra på är de väldigt bra på. Det är i huvudsak två områden där en kvantdator kan briljera:
- Simulera kvantmekaniska system. Vår värld är i allmänhet väldigt kvantmekanisk och ofta vill man simulera olika system för att försöka förstå hur världen fungerar. Det har visat sig vara väldigt svårt att simulera sådana system med en klassisk dator eftersom simulationen växer exponentiellt då systemet växer. En kvantdator däremot är i sig ett kvantmekaniskt system, vilket innebär att den kan simulera kvantmekaniska system oerhört mera effektivt än en klassisk dator. Problem i den här kategorin kräver ofta inte heller lika många qubitar som problem i kategori 2.
- Optimeringsproblem. En kvantdator kan vara väldigt effektiv på att hitta den “bästa” lösningen till problem. Ett bra exempel av ett optimeringsproblem är travelling salesman – problemet, där en handelsman ska besöka ett visst antal städer genom att gå den kortaste rutten. Problemet är väldigt svårt att lösa för en klassisk dator då antalet städer blir stort, eftersom den måste gå genom alla möjliga sträckor och kolla vilken som blir kortast. Det är för tillfället oklart om en kvantdator kan specifikt lösa travelling salesman – problemet effektivare.
Ett område som redan tagit stor nytta av kvantdatorer är beräkningskemin. Beräkningskemi faller in i kategori 1, d.v.s. att simulera kvantmekaniska system. Det har redan länge existerat algoritmer för att simulera och lösa kemiska problem, men störningarna hindrar fortfarande framsteg. För att besegra dessa tappra störningar har man trollat fram en hybrid kvant-klassisk algoritm för att minska på kretsarnas längd. (Kom ihåg att en kort krets är en stabil krets.) Inom fysiken har man redan lyckats simulera enklare kvantmekaniska system som “Hubbard modellen” eller “Ising modellen” där man simulerar elektroner i gitter.
Nästa artikel avslöjar vad framtiden kan ha att erbjuda. En perfekt kvantdator: Uhka vai mahdollisuus? Stay tuned.