I artikeln Matematikhörnan: Delbarhet definierades delbarhetssekvenser för naturliga tal. Delbarhetssekvensen för det naturliga talet  består av talen
består av talen 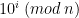 , där
, där 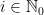 . I nedanstående tabell ser vi början av delbarhetssekvenserna för några tal:
. I nedanstående tabell ser vi början av delbarhetssekvenserna för några tal:
- 2: 1, 0, 0, 0, 0, 0…
- 3: 1, 1, 1, 1, 1, 1…
- 5: 1, 0, 0, 0, 0, 0…
- 7: 1, 3, 2, -1, -3, -2…
- 9: 1, 1, 1, 1, 1, 1…
- 11: 1, -1, 1, -1, 1, -1…
I föregående artikel märkte vi att alla av dessa sekvenser kommer att upprepa sig i något skede. För talen 2 och 5 beror detta på att något av talen är noll, och därmed kommer alla därpåföljande tal att vara noll, ty ifall 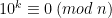 , så är även
, så är även 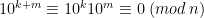 .
.
De övriga sekvenserna i tabellen innehåller talet 1 på något annat index än 0. Då upprepas sekvensen, eftersom om  , så gäller
, så gäller 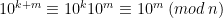 .
.
Alltså, ifall en sekvens innehåller talet 0 eller 1 på något annat index än 0, kommer sekvensen att upprepas.
Sekvenser som innehåller talet 0
För att delbarhetssekvensen för talet  skall innehålla talet 0, måste det för något
skall innehålla talet 0, måste det för något  gälla att
gälla att
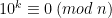 , dvs.
, dvs.  .
.
Eftersom 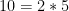 , kan detta gälla endast ifall talet
, kan detta gälla endast ifall talet  innehåller endast primtalsfaktorerna 2 och 5, dvs. om
innehåller endast primtalsfaktorerna 2 och 5, dvs. om
 , där
, där  .
.
Ifall  kan skrivas i ovanstående form, och vi betecknar
kan skrivas i ovanstående form, och vi betecknar 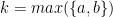 , gäller
, gäller  .
.
Sekvenser som innehåller talet 1
I vilka fall kan vi då vara säkra på att ett tal har en delbarhetssekvens som på något index olika noll har talet 1? Antag att 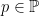 är ett primtal. Ifall
är ett primtal. Ifall  ej är talet 2 eller 5, kommer
ej är talet 2 eller 5, kommer  inte att dela talet
inte att dela talet 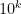 för något
för något  , alltså är
, alltså är  för alla
för alla  .
.
Som bekant bildar modulo-operationen  ringen
ringen  . Eftersom
. Eftersom  om p inte är primtalet 2 eller 5, gäller det att
om p inte är primtalet 2 eller 5, gäller det att 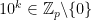 . Dessutom vet vi att om (och endast om)
. Dessutom vet vi att om (och endast om)  är ett primtal, är ringen
är ett primtal, är ringen  en kropp, alltså har alla tal förutom noll en multiplikativ invers. Detta är ekvivalent med att
en kropp, alltså har alla tal förutom noll en multiplikativ invers. Detta är ekvivalent med att  bildar en grupp med multiplikationsoperationen.
bildar en grupp med multiplikationsoperationen.
Delbarhetssekvensen består per definition av talen 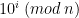 , där
, där 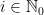 . I fallet där
. I fallet där  är ett primtal olika 2 och 5, innehålls alla tal i sekvensen alltså i den delgrupp av
är ett primtal olika 2 och 5, innehålls alla tal i sekvensen alltså i den delgrupp av  som talet
som talet 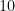 (eller närmare sagt dess ekvivalensklass) genererar. Eftersom gruppen
(eller närmare sagt dess ekvivalensklass) genererar. Eftersom gruppen  är ändlig, kommer även den genererade delgruppen att vara ändlig. Därmed existerar det ett
är ändlig, kommer även den genererade delgruppen att vara ändlig. Därmed existerar det ett  för vilket
för vilket 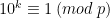 .
.
Talen i sekvensen kommer alltså att upprepas efter ett visst index k. Närmare sagt, eftersom 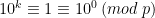 , sä gäller
, sä gäller
$latex \begin{array}{ll}
10^{k+1} \equiv 10^k10^1 \equiv 10^1\\
10^{k+2} \equiv 10^k10^2 \equiv 10^2\\
…\\
10^{k+k-1} \equiv 10^k10^{k-1} \equiv 10^{k-1}\\
\end{array}$ (mod p)
Sekvensen består alltså av cykler med längden k. Eftersom elementen i cykeln bildar en delgrupp av  , och gruppen
, och gruppen  har p-1 element, vet vi enligt Lagranges sats att cykelns längd delar talet p-1. Vi ser också att eftersom
har p-1 element, vet vi enligt Lagranges sats att cykelns längd delar talet p-1. Vi ser också att eftersom  , kommer cykeln att starta från det första talet (alltså talet
, kommer cykeln att starta från det första talet (alltså talet  ) i sekvensen. Sekvensen har alltså ingen s.k. svans före cykeln.
) i sekvensen. Sekvensen har alltså ingen s.k. svans före cykeln.
Alltså alla primtal utom 2 och 5 har ett index olika noll på vilket delbarhetssekvensen har värdet 1. Naturligtvis kan även icke-primtal ha talet 1 i sin sekvens; i tabellen ovan ser vi att detta gäller för talet 9.
Övriga fall
Vi kan vara säkra på att delbarhetssekvensen för talet  (icke-trivialt) innehåller talet 1 endast om
(icke-trivialt) innehåller talet 1 endast om  är ett primtal. Därmed kunde man förvänta sig att det existerar tal vars delbarhetssekvens innehåller varken talet 0 eller talet 1. Det visar sig att detta gäller för talet 6. Låt oss alltså undersöka dess delbarhetssekvens:
är ett primtal. Därmed kunde man förvänta sig att det existerar tal vars delbarhetssekvens innehåller varken talet 0 eller talet 1. Det visar sig att detta gäller för talet 6. Låt oss alltså undersöka dess delbarhetssekvens:
För talet 10 gäller det att
 ,
,
och därmed ser vi att
 .
.
Av detta följer naturligtvis direkt att
 .
.
Alltså är delbarhetssekvensen för talet 6 1,-2,-2,-2,… och sekvensen upprepar sig själv, fastän den inte icke-trivialt innehåller talet 0 eller 1.
Vad kan vi då säga om delbarhetssekvensen för talet  som ej är ett primtal och har andra primtalsfaktorer än 2 och 5? Som vi redan tidigare konstaterat, bildar modulo-operationen
som ej är ett primtal och har andra primtalsfaktorer än 2 och 5? Som vi redan tidigare konstaterat, bildar modulo-operationen  ringen
ringen  . Ringen är nu inte en kropp, eftersom vi antog att
. Ringen är nu inte en kropp, eftersom vi antog att  inte är ett primtal. Vi vet dock ändå att ifall vi multiplicerar två tal i ringen, kommer resultatet även att befinna sig i ringen.
inte är ett primtal. Vi vet dock ändå att ifall vi multiplicerar två tal i ringen, kommer resultatet även att befinna sig i ringen.
Vi har alltså endast n stycken olika möjliga multiplikationsresultat. Därmed om vi beräknar talen  , där
, där 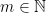 , måste vi i något skede stöta på ett tal som förekommit tidigare i sekvensen. Vi vet även att detta händer senast, då
, måste vi i något skede stöta på ett tal som förekommit tidigare i sekvensen. Vi vet även att detta händer senast, då 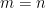 , eftersom vi inte kan ha
, eftersom vi inte kan ha 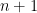 olika tal i ringen. Alltså, vi hittar ett tal
olika tal i ringen. Alltså, vi hittar ett tal 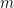 och ett annat tal
och ett annat tal  för vilka
för vilka
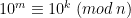 .
.
Av detta följer naturligtvis att
$latex \begin{array}{ll}
10^{m+1} \equiv 10^m10^1 \equiv 10^k10^1 \equiv 10^{k+1}\\
10^{m+2} \equiv 10^m10^2 \equiv 10^k10^2 \equiv 10^{k+2}\\
…\\
10^{m+(m-k)-1} \equiv 10^{k+(m-k)-1} \equiv 10^{m-1}\\
10^{m+(m-k)} \equiv 10^{k+(m-k)} \equiv 10^k\\
\end{array}$ (mod n),
alltså går sekvensen efter talet 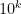 in i en cykel med längden
in i en cykel med längden  . Till skillnad från sekvenserna för primtal, kan denna sekvens ha en s.k. svans i början förrän cykeln börjar. Detta beror på att talet 1 inte nödvändigtvis förekommer i sekvensen förutom i början.
. Till skillnad från sekvenserna för primtal, kan denna sekvens ha en s.k. svans i början förrän cykeln börjar. Detta beror på att talet 1 inte nödvändigtvis förekommer i sekvensen förutom i början.
Öppna frågor
Talen 3 och 9 har exakt likadan delbarhetssekvens; den består endast av ettor. Finns det andra talpar som har exakt likadan delbarhetssekvens? Om det finns, kan vi hitta något samband för tal som har likadan delbarhetssekvens?
Finns det något samband mellan primtalsutvecklingen och delbarhetssekvensen för tal?
Kan vi på något vettigt sett gruppera icke-primtal i olika grupper, t.ex. enligt längden på cykeln?
Litteratur
Allmän algebra:
Jokke Häsä, Johanna Rämö: Johdatus abstraktiin algebraan, Gaudeamus, 2012.
Tauno Metsänkylä, Marjatta Näätänen: Algebra, Limes, 2005.
Nyttiga wikipedia-länkar:
Group
Ring
Finite field (ändlig kropp)
Lagrange’s theorem
Fundamental theorem of arithmetic



