Sudoku, eller “Number Place” som det ursprungligen hette är i dagens läge ett mycket välkänt logiskt pussel:


Givet ett  rutfält delvis ifyllt av siffrorna
rutfält delvis ifyllt av siffrorna  skall du fylla i resten av rutorna med siffrorna
skall du fylla i resten av rutorna med siffrorna  så att varje siffra uppkommer endast en gång på varje rad/kolumn/liten ruta, vilka i exemplet omringas i bilden av de lite tjockare linjerna.
så att varje siffra uppkommer endast en gång på varje rad/kolumn/liten ruta, vilka i exemplet omringas i bilden av de lite tjockare linjerna.
Sudoku pussel kan hittas överallt; många tidningar (t.ex. Hbl) publicerar sudokun dagligen, dessutom kryllar bokaffärerna av ”traditionella” och internet av elektroniska sudokun i varierande kvalitet. För de allra ivrigaste lösarna ordnas det årligen VM, med tusentals euron som pris. För den intresserade läsaren finns det i källorna ett par länkar om sudokuns historia, jag måste medge att jag hade trott att sudoku skulle härstamma från Japan, men den moderna varianten av sudoku skapades (högst troligen) av en 74-årig arkitekt från USA.
Det skulle kunna finnas ett antal olika aspekter att diskutera då det kommer till sudokun. Jag kommer att (igen) ta en datavetar-syn på det hela och undersöka till vilken grad datorer kan användas för sudokulösning. Det vill säga: hur svårt är lösning av sudokun för en dator och har människan någon chans klara sig mot dem? Mer specifikt så kommer jag att presentera tre olika algoritmer för sudokulösning samt jämföra dem med varandra.
Sudokulösning med datorhjälp
Näst går vi alltså igenom tre alternativa algoritmer för att lösa sudokun. För läsbarhetens skull kommer jag inte att gå in på detalj då det kommer till implementeringen av de mer komplicerade algoritmerna. Detaljerad förståelse för algoritmerna krävs inte i resten av texten och för de intresserade läsarna finns det en bilaga med (lite) mer detalj.
Algoritm 1: SimpleSolver
Den första algoritmen vi undersöker är också den enklaste. Ifall jag skulle be 100 människor beskriva det simplaste sättet de kommer på för att lösa sudokun, skulle de flesta högst troligen beskriva SimpleSolver. Det handlar nämligen om att pröva alla de (ändligt många) sätten att fylla i de tomma rutorna. Algoritmen fungerar genom att gå igenom alla tomma rutor en åt gången och pröva alla möjliga siffror att sätta i dem. Efter att ha fyllt rutan granskar algoritmen att alla sudokuregler fortfarande uppfylls. Om allt är ok går algoritmen vidare till nästa tomma ruta, annars prövar algoritmen nästa siffra. Om algoritmen tvingas pröva alla siffror utan att kunna hitta en lösning går den tillbaka till föregående tomma ruta och prövar nästa siffra.
Med denna taktik kommer algoritmen i något skede att ha prövat alla möjligheter och därmed också hittat lösningen. SimpleSolver är väldigt simpel, implementation av den brukar vara en av räkneövningarna under grundprogrammeringskurserna i Gumtäkt.
Algoritm 2: DLXSudoku
Till skillnad från första algoritmen är de två andra algoritmerna för sudokulösning ursprungligen inte skapade för sudokun. Istället baserar de sig på idén att omvandla sudoku problemet till något annat (välkänt) problem och sedan lösa det andra problemet istället. Orsaken till att vilja göra såhär är att det ofta är lättare att omvandla problem än att lösa dem. Så om vi kan hitta andra problem som någon annan (lite fiffigare) människa har utvecklat effektiva lösningsalgoritmer för, kan vi dra nytta av dessa algoritmer genom att omvandla vårt problem. Detta är ofta tidseffektivare än att tillbringa en massa tid på att utveckla specialiserade algoritmer för just sudokun. Inom datavetenskap kallar man ofta denna process för en reduktion av ett problem till ett annat. Vår andra algoritm är baserad på en reduktion av sudokun till exact cover problemet och lösning av exact cover med hjälp av Algoritm X implementerad med dancing links: DLXSudoku.
Exact cover är ett ganska abstrakt problem: Givet en matris bestående av endast ettor och nollor är uppgiften att välja ut en delmängd av raderna i matrisen så att det bland de rader vi väljer ut finns exakt en etta i varje kolumn (Obs! Detta är inte den mest allmänna formuleringen av exact cover, men tillräcklig för vårt behov). Ett sudoku problem kan relativt enkelt omvandlas till en exact cover matris :
- Varje tom ruta i sudokubrädet motsvaras av 9 rader i matrisen. Vi kallar dessa rader för
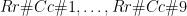 där den tomma rutan i fråga finns på rad r kolumn c.
där den tomma rutan i fråga finns på rad r kolumn c.
- Kolumnerna i matrisen representerar de olika sudoku reglerna:
- Varje ruta i sudokubrädet skall få exakt 1 siffra
- Varje kolumn på sudokubrädet skall bli ifylld av exakt en av varje siffra
- Varje rad i sudokubrädet skall skall bli ifylld av exakt en av varje siffra.
- Varje liten ruta skall bli ifylld av exakt en av varje siffra.
Alla av dessa regler representeras av kolumnerna så att kolumnen innehåller en etta på alla rader som uppfyller regeln (se exempel nedan).
Efter denna konstruktion kan vi lösa exakt cover problemet och omvandla lösningen till en lösning av sudokut helt enkelt genom att fylla i sudokut enligt de rader Rr#Cc#x som vi valt ut till exact cover lösningen. Notera specifikt att kolumnerna i exact cover matrisen som representerar kravet ”varje ruta på sudokubrädet får exakt ett värde” försäkrar oss om att exact cover lösningen innehåller för varje rad r och kolumn c på sudoku brädet, exakt en rad Rr#Cc#i från exact cover matrisen. För den intresserade läsaren finns det som bilaga till denna text en beskrivning på hur DLX fungerar. Här nöjer vi oss med att nämna att algoritmen har populariserats av Donald Knuth, som även har utvecklat det (inom naturvetenskaper) mycket använda LateX typsättningssystemet.

Exempel: Vi reducerar  sudokut ovanför till exact cover. För detta sudoku får vi en exact cover matris med
sudokut ovanför till exact cover. För detta sudoku får vi en exact cover matris med 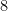 (antalet tomma rutor)
(antalet tomma rutor) 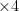 rader. Bilden nedan visar en del av den:
rader. Bilden nedan visar en del av den:
 I bilden representerar första kolumnen kravet: ”Rutan på rad 2 kolumn 1 måste få exakt 1 värde”. Vi ser att kolumnen innehåller en etta på varje rad vars val fyller i rutan och 0 annars. Andra kolumnen representerar kravet ”Någon ruta på rad två måste innehålla en etta”, tredje kolumnen representerar: ”Första kolumnen måste innehålla en fyra” och fjärde ”lilla rutan uppe till höger måste innehålla en etta”, vi märker specifikt att fjärde kolumnen innehåller en etta endast på första raden. Detta betyder att vi måste välja första raden till exact cover lösningen vilket i sin tur betyder att rutan i kolumn 1 rad 2 kommer att innehålla en etta.
I bilden representerar första kolumnen kravet: ”Rutan på rad 2 kolumn 1 måste få exakt 1 värde”. Vi ser att kolumnen innehåller en etta på varje rad vars val fyller i rutan och 0 annars. Andra kolumnen representerar kravet ”Någon ruta på rad två måste innehålla en etta”, tredje kolumnen representerar: ”Första kolumnen måste innehålla en fyra” och fjärde ”lilla rutan uppe till höger måste innehålla en etta”, vi märker specifikt att fjärde kolumnen innehåller en etta endast på första raden. Detta betyder att vi måste välja första raden till exact cover lösningen vilket i sin tur betyder att rutan i kolumn 1 rad 2 kommer att innehålla en etta.
Algoritm 3: SATSudoku
Den sista av våra algoritmer reducerar sudoku till det kanske mest kända ”svåra” problemet inom datavetenskap, nämligen satisfiability (SAT). För att kunna beskriva SAT måste vi påminna oss om logik kursen i gymnasiet och specifikt de delarna som handlade om propositionslogik.
Propositionslogik är ett väldigt enkelt logiskt ”språk” där man formar formler genom att binda ihop sanningsvariabler (dvs. variabler som antingen kan vara sanna eller falska) med hjälp av 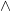 (OCH),
(OCH), 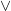 (ELLER) och
(ELLER) och  (INTE). (Obs. det finns ett antal olika sätt att definiera propositionslogik, vi använder det simplaste möjliga som räcker för vårt behov). Givet en propositionslogisk formel går SAT problemet ut på att hitta ett sätt att ge sanningsvärden (sant eller falskt) åt variablerna som gör att hela formeln blir sann. Sanningsvärdet för en formel definieras utgående från sanningsvärden för de delformler den innehåller:
(INTE). (Obs. det finns ett antal olika sätt att definiera propositionslogik, vi använder det simplaste möjliga som räcker för vårt behov). Givet en propositionslogisk formel går SAT problemet ut på att hitta ett sätt att ge sanningsvärden (sant eller falskt) åt variablerna som gör att hela formeln blir sann. Sanningsvärdet för en formel definieras utgående från sanningsvärden för de delformler den innehåller:
- Om formeln endast består av en enda variabel är dess sanningsvärde lika med sanningsvärdet för variabeln.
- Sanningsvärdet för
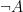 är motsatsen till sanningsvärdet för formeln
är motsatsen till sanningsvärdet för formeln 
- Formeln
 är sann ifall både formlerna
är sann ifall både formlerna  och
och 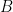 är sanna
är sanna
- Formeln
 är sann ifall antingen
är sann ifall antingen  eller
eller 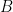 (eller båda) är sanna.
(eller båda) är sanna.
Då vi i denna text pratar om att lösa SAT menar vi att hitta ett sätt att ge värden åt variablerna i en given formel så att formeln blir sann. Vi kallar detta sättet för en ”lösning” av SAT. (Notera att detta inte är en allmän definition av SAT problemet, men tillräcklig för oss.)
SAT är ett mycket välkänt problem inom datavetenskap. I dagens läge existerar det effektiva algoritmer för att lösa formler som består av hundratusentals variabler och miljontals delformler. För att kunna använda dessa algoritmer för att lösa sudokun måste vi från ett givet sudokubräde kunna forma en propositionsformel som tillåter oss omvandla en lösning på SAT problemet till en lösning på sudoku problemet.
För varje ruta, säg på rad r kolumn c, introducerar vi 9 sanningsvariabler:  . Meningen med dessa variabler är: ”
. Meningen med dessa variabler är: ”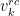 är sann om och endast om rutan på rad r kolumn c får värdet k i sudokulösningen”. Vår formel kommer att bestå av 5 olika delformler, fyra olika beskrivningar på de olika sudokureglerna och en som beskriver de siffror som är färdigt ifyllda:
är sann om och endast om rutan på rad r kolumn c får värdet k i sudokulösningen”. Vår formel kommer att bestå av 5 olika delformler, fyra olika beskrivningar på de olika sudokureglerna och en som beskriver de siffror som är färdigt ifyllda:
1) Varje ruta skall få exakt ett värde. För en fixerad ruta på rad r kolumn c beskrivs detta krav av en logisk representation av: 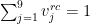 . Det finns olika sätt att representera detta som propositionslogik. Ett av de simplaste är att använda formeln:
. Det finns olika sätt att representera detta som propositionslogik. Ett av de simplaste är att använda formeln: 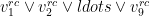 för att se till att rutan får minst ett värde och
för att se till att rutan får minst ett värde och  formler av formen:
formler av formen:  för att se till att den får högst ett värde. I vår implementation använder vi oss av ett lite annorlunda sätt att representera samma sak (kallas för sequential counter). För den intresserade läsaren finns det referenser.
för att se till att den får högst ett värde. I vår implementation använder vi oss av ett lite annorlunda sätt att representera samma sak (kallas för sequential counter). För den intresserade läsaren finns det referenser.
2) Varje rad skall få en av varje värde. För en fixerad rad R beskrivs detta av (del)formeln:
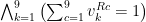
som omvandlas till propositionslogik precis som i punkt 1.
3) Varje kolumn skall få en av varje värde. För en fixerad column C beskrivs detta av formeln:
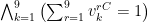
4) Varje liten ruta skall få en av varje värde. För t.ex. lilla rutan längst upp till vänster beskrivs detta av formeln:
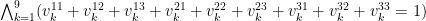
5) Varje redan färdigt ifylld ruta motsvaras av en formel som tvingar motsvarande variabel att sättas till sant. Så ifall rutan på rad r kolumn c har färdigt ifyllt värdet k lägger vi med delformeln 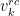 till hela formeln.
till hela formeln.
Vår sista algoritm för sudokulösning bygger upp ett SAT problem såhär och ger den åt en SAT algoritm. Så länge ursprungliga sudokut har en lösning kommer SAT algoritmen att hitta en lösning på SAT problemet. Sedan omvandlas SAT lösningen till en sudoku lösning: rutan på rad r kolum c i sudokubrädet fylls i med det värde k för vilket variabeln 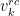 är sann i SAT lösningen. Delformeln vi satt med i punkt 1 här ovan försäkrar oss om att det finns exakt en sådan för varje tom ruta.
är sann i SAT lösningen. Delformeln vi satt med i punkt 1 här ovan försäkrar oss om att det finns exakt en sådan för varje tom ruta.

Exempel: Vi fortsätter med samma exempel som tidigare. Fullständiga propositionsformeln som beskriver detta exempel är för lång för att skrivas ner för hand. Men här följer en del illustrerande exempel
- Rutan på rad 2 kolumn 1 skall få exakt ett värde:
 .
.
- Kolumn 1 måste innehålla en etta:
 .
.
- Rad 1 måste innehålla en två:
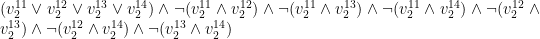 .
.
- Vissa rutor är färdigt ifyllda:
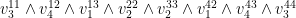 .
.
Bilagan till denna artikel går in på (lite mer) detalj om hur en SAT algoritm oftast fungerar.
Vilken är bäst?
Nu är det dags för den mest intressanta frågan; vilken är bäst? För att kunna testa detta fick jag hjälp av Toffe som implementera SimpleSolvern och Lasse som implementera DLXSudoku. Själv implementerade jag SATSudoku. Tack till både Toffe och Lasse!
Innan vi går till resultaten vill jag påpeka att skillnaderna vi kommer att se i dessa algoritmer inte beror på implementationerna, resultaten kan inte och skall inte användas för att jämföra våra kodningskunskaper.
Jag valde på måfå ut 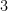 sudokun av storlek
sudokun av storlek  och tog tid på hur länge var och en av våra algoritmer tog på sig för att lösa dem. Resultaten finns nedan:
och tog tid på hur länge var och en av våra algoritmer tog på sig för att lösa dem. Resultaten finns nedan:

Det var ju lite tråkigt inte sant? Till och med den simplaste algoritmen löser alla 3 på under 1.5s, de mer avancerade lösarna tar under en tiondels sekund på sig. Detta illustrerar orsaken till varför jag bara hade tre sudokun; faktum är att de allra flesta normala sudokun är så gott som triviala för en dator. Det går att designa problem som vår SimpleSudoku inte skulle kunna lösa, men redan genom att ha SimpleSudoku pröva siffror i slumpmässig ordning istället för storleksordning så klarar även den av så gott som alla  sudokun snabbare än vad det skulle ta för människan att skriva ner en färdig lösning. Så det ser inte så hemskt lovande ut för oss människor.
sudokun snabbare än vad det skulle ta för människan att skriva ner en färdig lösning. Så det ser inte så hemskt lovande ut för oss människor.
Det verkar alltså klart att om man behöver få många sudokun löst snabbt är det mer tidseffektivt att koda en lösare än att lösa dem själv. Dock kan man efter dessa resultat fråga sig varför man över huvudtaget borde sätta ner tid på att implementera något som helst mer avancerat än SimpleSudoku?
Ifall man bara är intresserad av  sudokun är svaret: man borde inte. Men, om vi tillåter större sudokun blir saker och ting intressantare. Forskningsresultat inom sudokulösning (ja, det finns sådana) pratar ofta om ordningen (rank) av ett sudoku. En normal sudoku är av ordning 3 och allmänt så skall en sudoku av ordning
sudokun är svaret: man borde inte. Men, om vi tillåter större sudokun blir saker och ting intressantare. Forskningsresultat inom sudokulösning (ja, det finns sådana) pratar ofta om ordningen (rank) av ett sudoku. En normal sudoku är av ordning 3 och allmänt så skall en sudoku av ordning  lösas på ett
lösas på ett 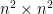 bräde. Så en
bräde. Så en  sudoku är av ordning
sudoku är av ordning 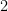 och en
och en 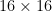 sudoku är av ordning
sudoku är av ordning 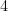 . Alla av våra algoritmer kan användas för att lösa sudokun av vilken ordning som helst. Dessutom borde större sudokun vara bättre för att jämföra algoritmer, intuitivt känns det ju ganska klart att ett större sudoku borde vara svårare än ett mindre.
. Alla av våra algoritmer kan användas för att lösa sudokun av vilken ordning som helst. Dessutom borde större sudokun vara bättre för att jämföra algoritmer, intuitivt känns det ju ganska klart att ett större sudoku borde vara svårare än ett mindre.

Resultaten finns ovan och nu börjar vi på riktigt märka skillnader i algoritmerna. SimpleSolvern klarade inte av en enda av dessa problem på under en timme (gränsen på lösningstiden). Däremot klarar sig både SATSudoku och DLXSudoku ganska väl, speciellt på ”enkla” sudokun. Av dessa två klarar sig SATSudoku lite bättre än DLX: den klarar av en ordning större ”lätt” problem och en ordning större ”svårt” problem.
Vad lär vi oss av detta? Jo, om du bara vill lösa ett enda normal stort sudoku är det fiffigare att ta papper och penna än börja koda. Skall du lösa 1000 normala sudokun kan du be datorn göra det på det enklaste möjliga sättet. Skall du lösa ett enkelt  sudoku, så går det också att fixas, dock med lite mer möda. Men om du vill lösa ett svårt
sudoku, så går det också att fixas, dock med lite mer möda. Men om du vill lösa ett svårt  sudoku? Då är det dags att ta fram pennan igen, skriva ett stort ”LÖS SJÄLV” på hela brädet, och ta en öl istället.
sudoku? Då är det dags att ta fram pennan igen, skriva ett stort ”LÖS SJÄLV” på hela brädet, och ta en öl istället.
Slutligen vill jag lämna er med det största sudokut som våra algoritmer klarade av och det minsta som de inte klarade. Om någon av er får någondera löst kan ni lämna en kommentar så sätter jag med er i resultaten.
Jeremias
BILAGA:
Algorithm X, Conflict Driven Clause Learning and Dancing Links for Sudokusolving.
Källor: