Jag tänkte kombinera ett av mina favoritspel med programmering och se vad jag kommer på. Spelet i fråga är go (kinesiska: wéiqí) och är ”känt för sin strategiska mångfald trots sina enkla regler” [Wikipedia: Go (brädspel)]. Reglerna till go kan förklaras på några minuter; om du inte tror på mig så kan du kolla följande video: Go – Basic Rules.
Du behöver egentligen bara veta följande tre regler:
- Man spelar turvis på skärningspunkterna av go brädet.
- Stenar som vidrör varandra räknas till en grupp. Diagonala stenar vidrör inte varandra.
- Då en grupp av stenar inte vidrör en enda tom punkt blir gruppen uppäten.
Med dessa simpla regler kan man t.ex. få till stånd en ”stege” som illustreras nedan:
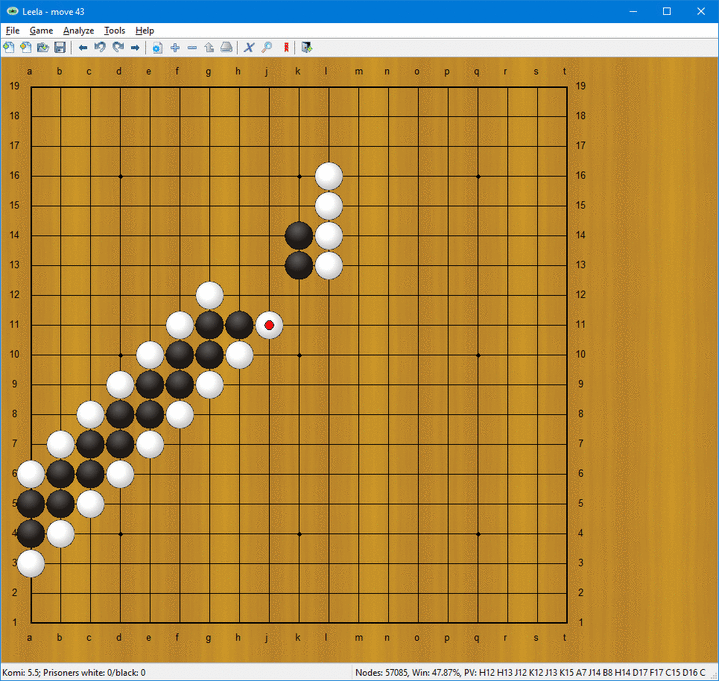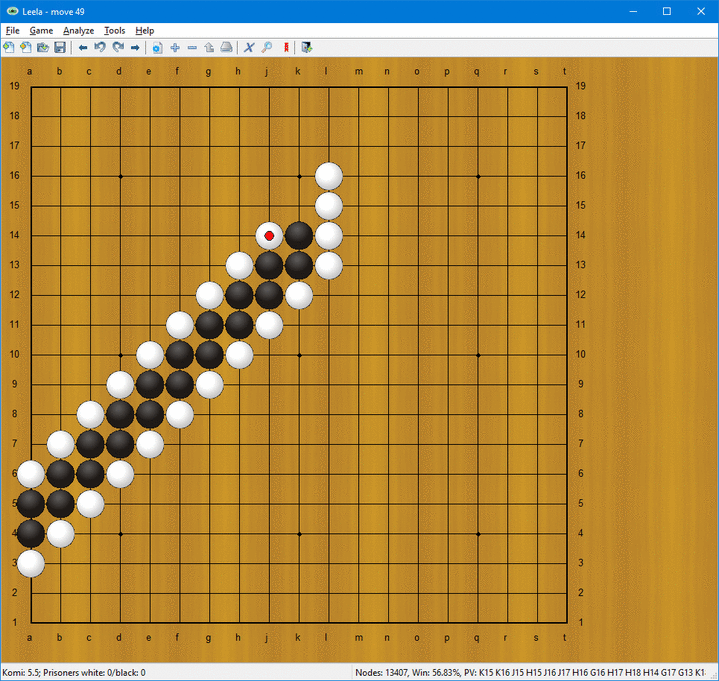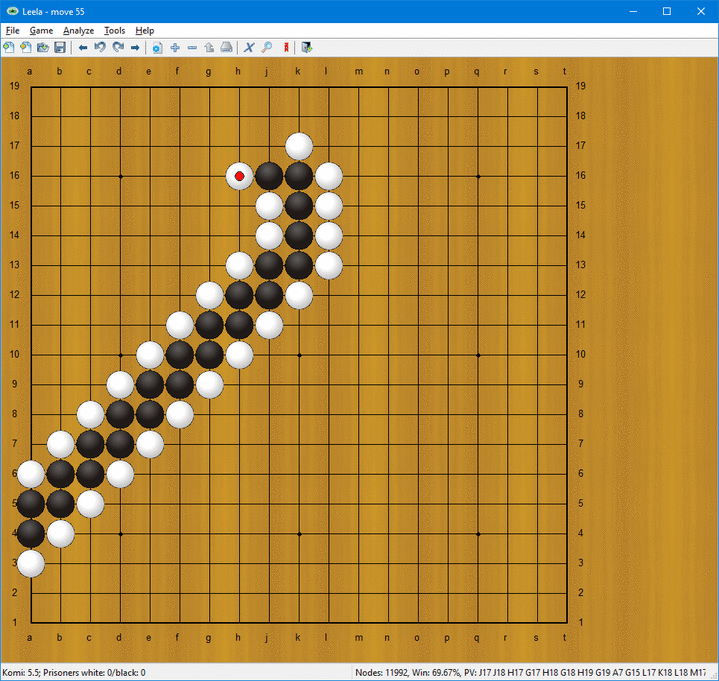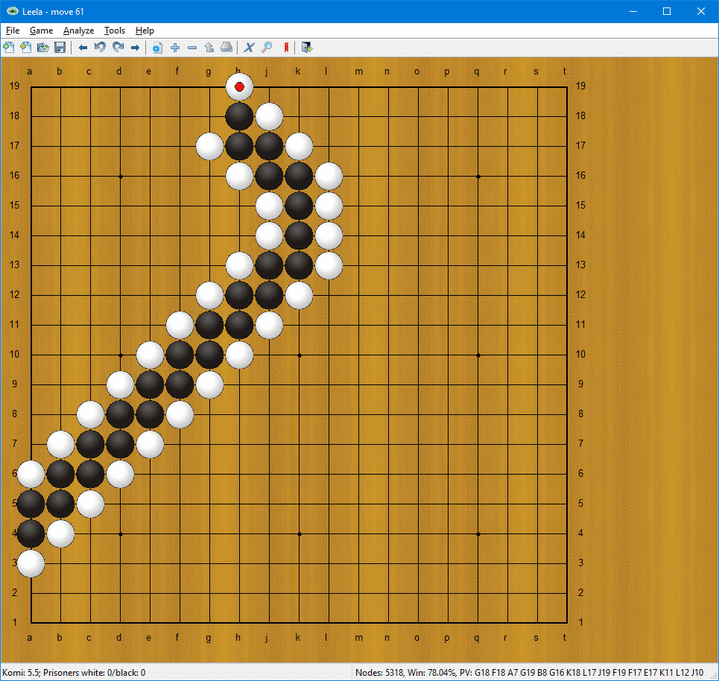
Efter varje vita drag måste svart svara med att spela utåt. Alla andra svarta drag leder till att vit kan omringa och äta upp den svarta stegen.
Med dessa simpla regler hittade jag på ett sätt att räkna saker — en go-kalkylator! Go-kalkylatorn fungerar på basis av stegarna jag nämnde tidigare. Spelbrädan kan vara av valfri storlek, och dit kan placeras vissa stenformationer på förhand. För att sparka igång kalkylatorn spelar man en vit sten så att den påbörjar en stege.
För kalkylatorn gäller dock två extra regler:
- Man skall spela ”kortsiktigt” och ”snålt” genom att alltid försöka hålla alla sina egna grupper i liv, och att inte ge motståndaren chansen att skydda deras grupper.
- I fall det finns flera stegar spelar man dem i tur och ordning.
Så hur utför man beräkningar? Följande saker kan utföras på stegen:
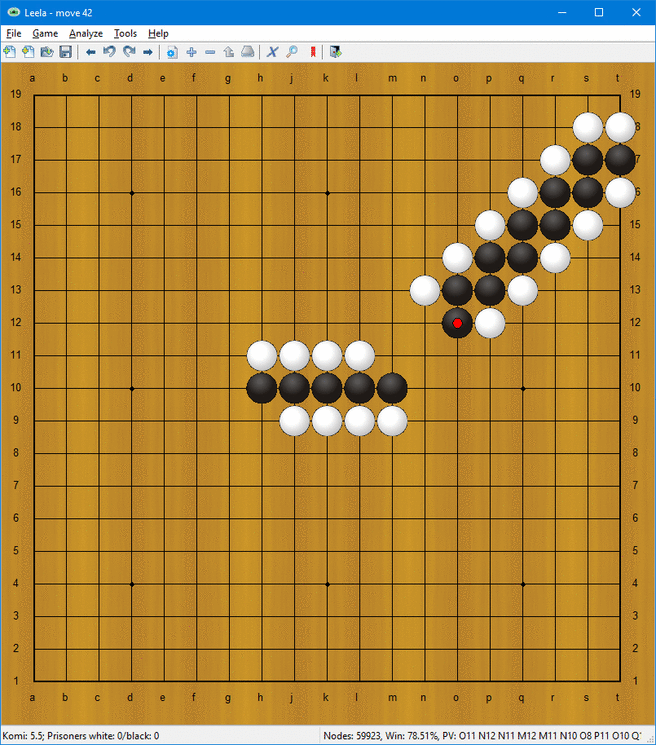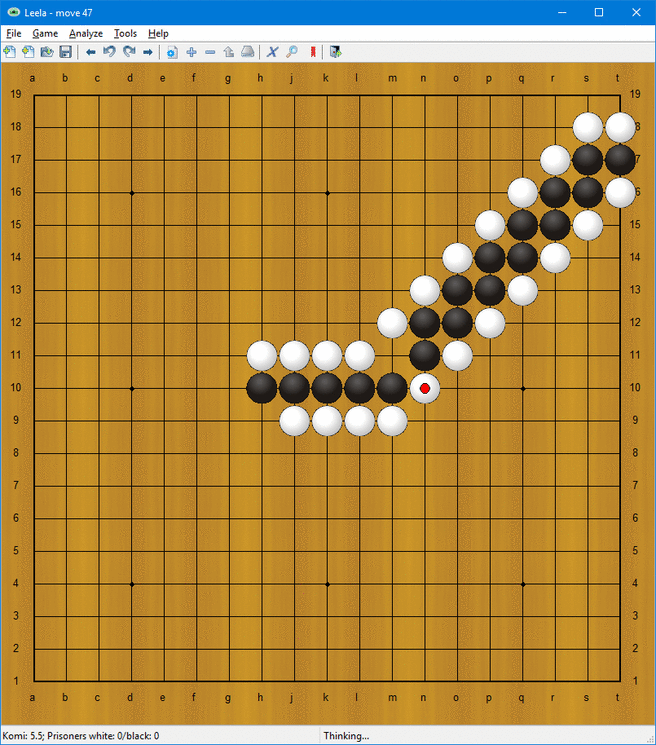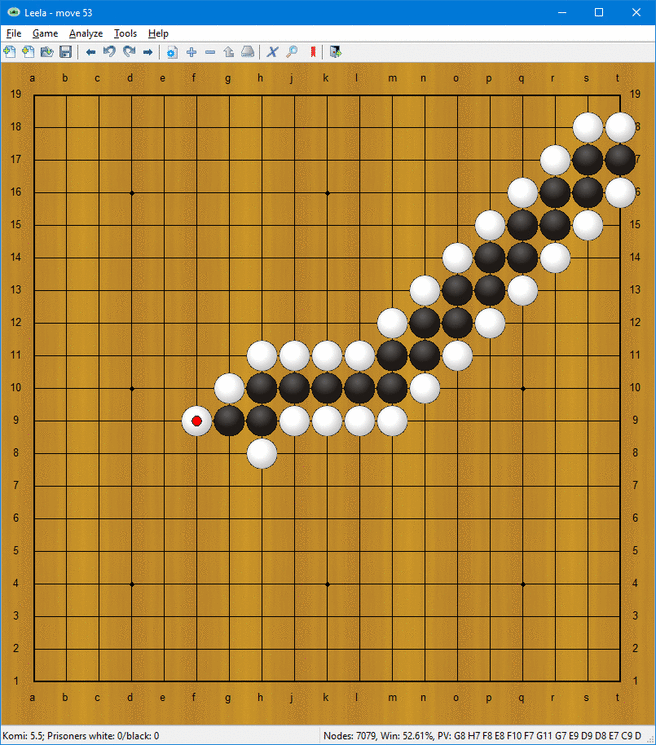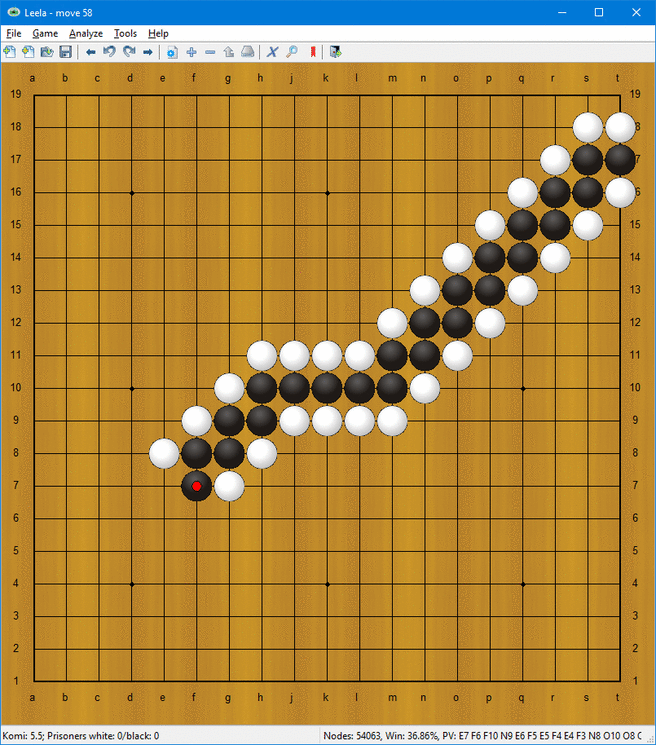
- Förflyttning och rotation (se också den första animationen)

- Duplikation
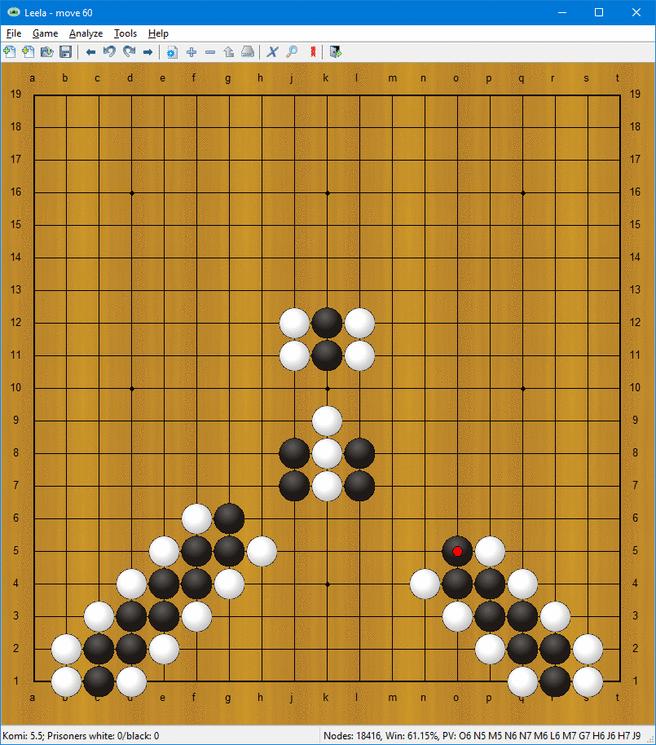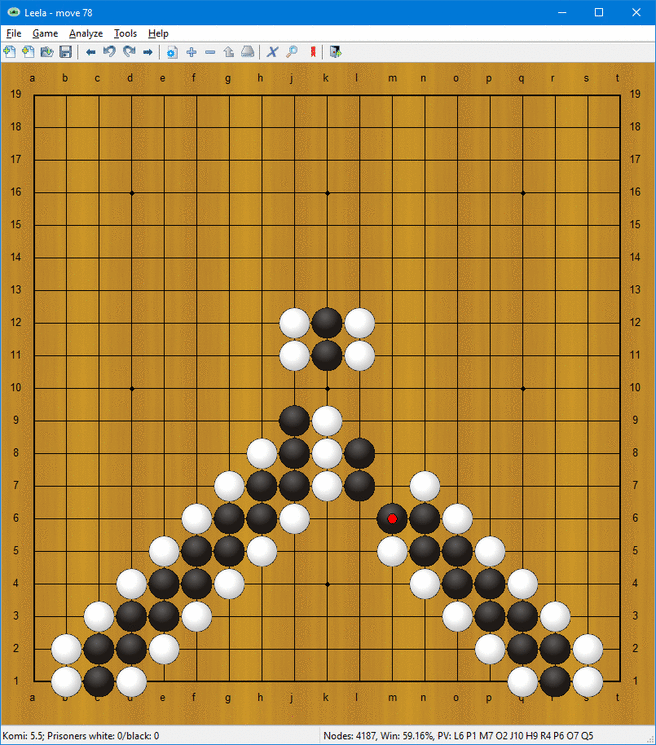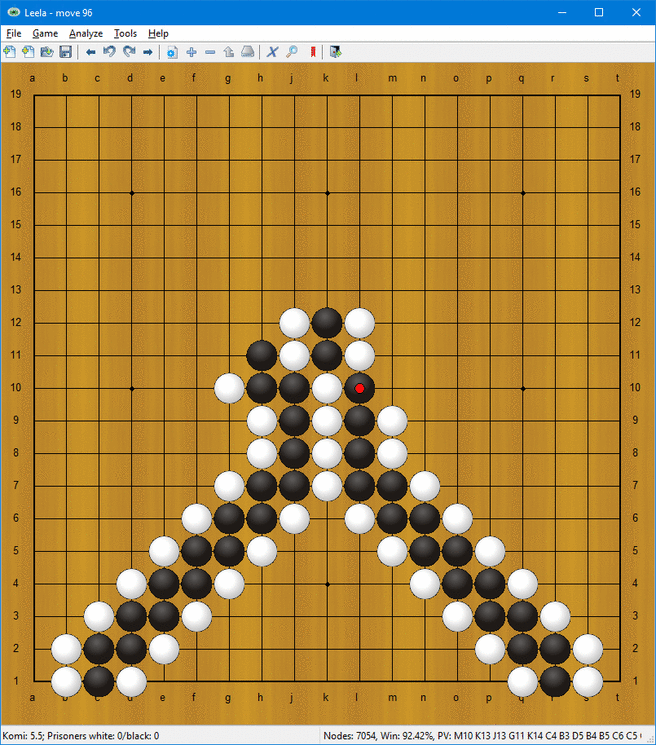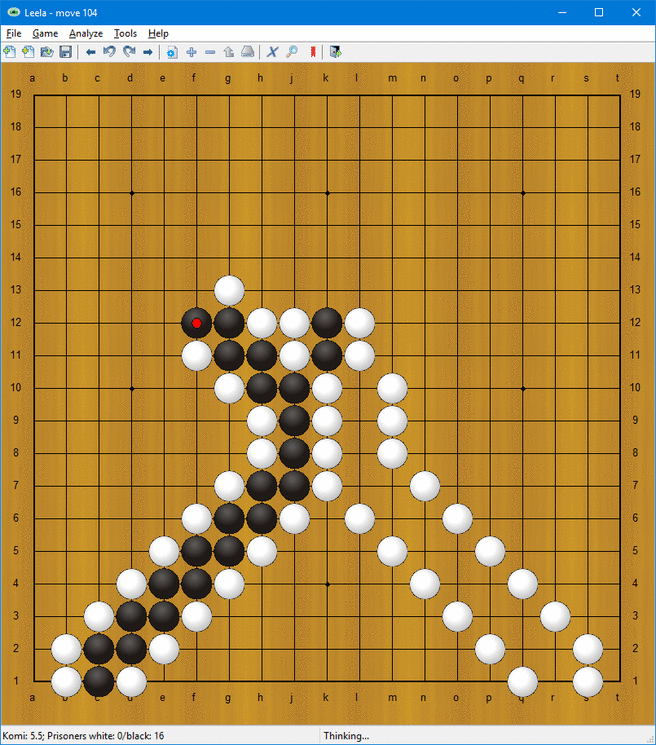
- Val av den första stegen som når en punkt
Den sista av dessa formationer möjliggör kalkyl. I animationen ovan följer stegarna den logiska satsen ”höger, och inte vänster”. Det vill säga att en stege som utvidgas högerut skapas bara då när en stege kommer från höger och ingen stege kommer från vänster.
Med en ”kontrollstege”, som sätts igång i början av programmet, kan man då skapa en steges X negation (”inte X”), som kan sedan användas för att räkna satser som ”X och Y” samt ”Y eller Z”. Med andra ord kan man beräkna alla simpla logiska satser.

Fast det skulle vara coolt att programmera en miniräknare på ett go-bräde så finns det ännu problemet med korsande stegar. Utan möjligheten att korsa stegar är kalkylationspotentialen starkt begränsat. T.ex. kan man skapa en 1+1 adderare, men troligtvis inte för större tal.