Kategoriarkiv: 2019

Texter från 2019

2019, Vecktraklet

Att simulera darts

Lämna en kommentar

Är du intresserad av att gå på idrottsevenemang men är trött på de höga biljettpriserna? Gör då som jag och simulera din favoritsport på datorn! Förutom att det är gratis så får du själv styra slutresultatet, alltså finns det endast fördelar med detta. I det här inlägget kommer jag att berätta om mitt simuleringsprogram och ett par resultat jag kom fram till.

Tavlan

Jag konstruerade tavlan enligt de dimensioner som definieras av WDF, dvs. World Darts Federation. Problemet med detta var att järnvajrarna som begränsar tavlans områden i verkligheten har en viss tjocklek, vilket skulle ha varit arbetsdrygt att ta i beaktande. Detta kan ha en liten betydelse då det gäller bredden på trippelringen i min tavla jämfört med dess verkliga bredd. Annars motsvarar min tavla en riktig darttavla.

Det är möjligt att double- och treble-ringarna är aningen smalare än i verkligheten.

Kastens avvikelse

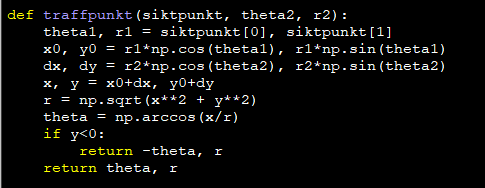
För att simulera kast och träffar lät jag varje kast avvika med avståndet r i en slumpmässig riktning från den egentliga siktpunkten, där r är ett slumpmässigt tal i [0, R] och R är ett tal som i förväg valts som maximal kastavvikelse. Denna metod fungerar relativt bra eftersom kasten hamnar då i en cirkel med flest träffar nära punkten man siktar på. Det som är dock nackdelen är att man i verkligheten har större missar i lodrät riktning jämfört med vågrät riktning. Därmed en bättre approximering skulle ha varit att konstruera kastcirkeln som en ellips.

Funktionen tar in en siktpunkt och en avvikelse som polära koordinater (\theta, r), beräknar dess summa och ger tillbaka den egentliga träffpunkten som en ny polär koordinat.

Resultat

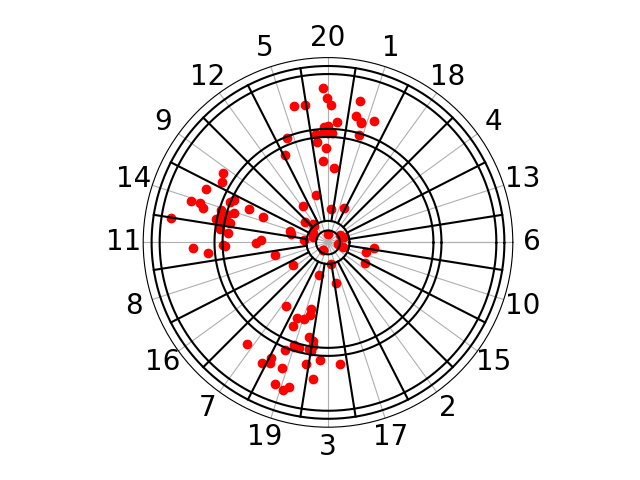
Då jag hade programmerat alla nödvändiga funktioner som gjorde det möjligt att visa och räkna poäng började jag med simuleringarna för att testa olika strategier. Som först ville jag jämföra olika områden på tavlan tillsammans med olika spridningar. Områdena var T20, T19, Bull samt området T11/T14. Mellan T11 och T14 är ett område jag ibland siktar på eftersom det är ett väldigt stabilt område. Om mitt kast är dåligt får jag ändå antagligen 8 eller 9 (se bild 1). Spridningarna jag testade på dessa områden var 2 cm, vilket motsvarar ungefär professionella spelarnas kast, 5 cm, som motsvarar ungefär mina kast, samt 17 cm vilket är tavlans radie. På varje område med varje spridning simulerade jag 1000 spel (totalt 12000), där ett spel går ut på att man kastar turer på tre pilar tills man går över 500p. Sedan jämförde jag medelvärdet av antalet turer som krävdes, och resultatet var följande:

T20T19BullT11/T14
2 cm5.2755.526.0747.806
5 cm9.019.0459.65610.296
17 cm15.17214.83112.24715.852

Kom ihåg att mindre värden är bättre. Från tabellen ser vi orsaken varför professionella siktar mer eller mindre alltid på T20. Då spridningen blir tillräckligt stor (väldigt stor) lönar det sig dock att sikta på bullen eftersom många pilar annars hamnar utanför tavlan.

Så här såg tavlan ut efter en simulering där man kastat et antal kast mot T20, T19, Bull och T11/T14.

Den huvudsakliga poängen är dock inte simuleringarnas resultat, utan främst att simulationen var en rolig utmaning för mig. Då man börjar vara trött på studierna (eller livet) kan det vara bra för sin egen motivation att utföra ett projekt som tangerar både ens studier och fritidsintressen. Under tiden jag kodade darttavlan lärde jag mig nya saker både inom matematik och programmering, och jag kommer inte på ett bättre sätt att göra detta.

2019, Vecktraklet

Hur man botar ”Writer’s block”

Lämna en kommentar
  1. Jag skriver inläggets rubrik och prokrastinerar sedan i en vecka.
  2. Bestämmer mig slutligen för att åstadkomma något, men vet inte vad ”Writer’s block” är på svenska.
  3. Det heter uppenbarligen ”skrivblockering”, enligt den oändligt pålitliga källan Wikipedia.
  4. Lär mig att tillståndet kan orsakas av prestationsångest eller brist på inspiration.
  5. Kollar meditationsguider på Youtube för att lära mig minska ångesten och ”öppna tankarna”.
  6. Inser snabbt att meditation inte fixar huvudet gratis, utan kräver övning för att ha någon positiv verkning.
  7. Eftersom deadlinen närmar sig, tar jag och prokrastinerar lite till.
  8. Startar en inre monolog utav frustration: ”Hur fan kan det vara så svårt att få nåt skrivet? Jag har ju gjort det förut, även med betydligt mindre tid att förbereda mig. Man kan ju rambla om vad som helst här i redaktionen, inte bryr dom sig vad man skriver. Nä helvete, jag förtjänar nog inte att vara med här…”
  9. Konstaterar att det föregående var överdramatiserat.
  10. Inser slutligen att det finns guider för behandling av skrivblockering som garanterat är bättre än vad jag kan åstadkomma.
  11. Som det visar sig är det OK att skriva skräp. Jag anser mig vara klar då jag märker att inlägget är exakt 200 ord långt. Tack och hej!
2019, Vecktraklet

Parentesfrågan

Lämna en kommentar

Läsaren har högst antagligen en uppfattning om vad parenteser är och vad deras roll är i en mening. Parenteser (trots namnet) är alltså inte teser, utan de ”… förtydligar, kommenterar, förklarar eller innebär ett sidospår från den övriga texten” (copy paste från Wikipedia). Med ”parenteser” menar jag förstås rundparenteser och inte hak-, klammer-, vinkel- eller piggparenteser, fastän samma grundprincip gäller också för dem.

Inom matematikens teoretiska drömvärld, till skillnad från naturliga språk, används parenteser för att ”ange grupper av termer […] för ordningen av räkneoperationer” (Wikipedia). Vi kan därmed säga att i matematiken har parenteserna olik semantik, vilket leder oss till en fråga: Vilken roll borde parenteser ha inom programmering?

Programmering är till stor del matematik. De första programmeringsstrukturerna härstammade från rena matematiska modeller som förverkligades med hjälp av elektronrör och senare mikroelektronik. Vi tar två konkreta exempel för att illustrera hur parenteser vanligtvis används inom programmering.

(defn kvadrat-summa [n]; summerar n första kvadraterna
 (loop [i 0 resultat 0]; sätter variablerna 'i' och 'resultat' som 0
  (if (<= i n)
   (recur (inc i) (+ resultat (* i i)))
   resultat
)))

(print (kvadrat-summa 5))

Ovan är Clojure kod som spottar ut summan på de fem första kvadrattalen. Clojure tillhör LISP familjen av programmeringsspråk där parenteser strukturerar programmet. Notera att all kod är omringad av parenteser som skapar en hierarki av funktioner och värden. Förklarningar och kommentarer placeras inte inom parenteser, utan inleds med semikolon. Koden kan köras här för de intresserade. 

!gfortran, gcc version 5.4.0 20160609
!Summerar n första kvadraterna
 integer function kvadrat_summa(n) result(summa)
     real :: lista(n)
     
     lista = (/(i, i=1,n, 1)/)
     lista = lista*lista
     summa = sum(lista)
 end function kvadrat_summa

 program P
     print *, kvadrat_summa(5)
 end program P

Som ett mindre extremt exempel på parenteser inom programmering kan vi betrakta ett bekant språk för fysiker, Fortran! Du kan köra koden här. Se hur parenteser används för att:

  • generera listor,
  • definiera funktionens resultat samt listans storlek, och
  • för att gruppera parametrar givna till funktioner.

Vi ser att parenteser behandlas liknande som inom matematiken, men varför så? Borde inte kod sträva efter att vara så naturligt läsbart som möjligt?

Svaret på första frågan är simpel; programmeringsspråk skapas av datanördar och inte lingvister. Men för att exemplifiera att naturliga parenteser är möjliga (och kanske även vettiga) inom programmering skrev jag nedan ett exempel på ett påhittat Python-liknande språk. Parenteserna fungerar som kommentarer eller tillägger extra detaljer.

(heltals) funktion kvadrat_summan på n (ett heltal):
  (summerar n första kvadraterna)
  i = 0
  resultat = 0
  medan i <= n:
    resultat += i * i
    i += 1
  resultat

visa kvadrat_summan på 5

Mycket snyggare och klarare kod, inte sant? Bara om nån skulle hitta på ett liknande språk som också är körbart…

Fortsättning följer!