Dags för ett litet ordspel!
Spelet liknar hänggubbe eller hängman, i och med att du skall gissa ett ord som bara jag vet. Du kan gissa bokstäver, ord eller delar av ord, exempelvis ”kaff”.
Jag måste svara på om din gissning finns i mitt ord. Om det dolda ordet är ”abrakadabra” och du gissar på ”bra” svarar jag jakande, men om du gissar ”arb” svarar jag nekande. Du får inte veta var i ordet din gissning förekommer.
Frågan är nu, vad är det snabbaste sättet att klura ut ordet? Några lösningar beskrivs nedan, läs på egen risk!
Att testa sig fram tar i genomsnitt 1/2 * bordn/(bA! bB! … bZ!) försök, där bord är mängden olika bokstäver som finns i ordet. Ordet ”abrakadabra” tar ungefär 1/2 * 2911/(5! 2! 2! 1! 1!) ~ 1.27 * 1013 försök. Ett Twitter-meddelande som inkluderar siffror och små bokstäver kan ta upp till 1.37 * 10210 försök.
Så istället för att bara hitta bokstäverna som förekommer i ordet och sedan testa oss fram, varför klurar vi inte ut alla 2-strängar (2 bokstäver långa teckensträngar) som finns i ordet? Kan vi då få reda på ordet snabbare? Svar: jo.
Att klura ut alla 2-strängar kräver högst B + bord * (bord-1) / 2 eller i värsta fall B/2 + B2/2 gissningar, där B är mängden användbara bokstäver. Detta tar inte så värst länge, men vad har man för nytta av 2-strängar? Kan man med hjälp av dessa bygga snabbt upp 3-strängar?
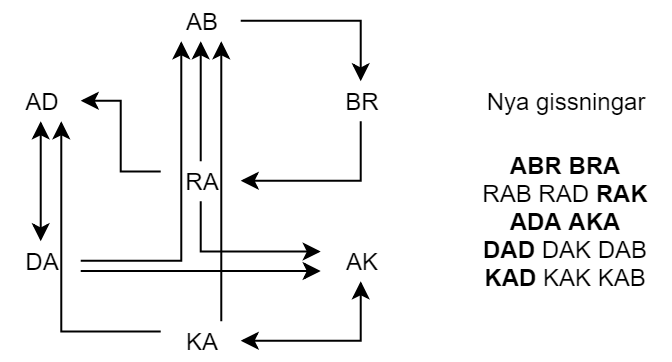
Genom att visualisera 2-strängar som en graf kan man skära bort flera onödiga gissningar. Noderna i grafen är alla 2-strängar vi känner till, och kanterna länkar strängarna till varandra så att följande sträng börjar med delsträngen som den första slutar med. Notera att mängden olika k-strängar av ordet inte kan vara mer än n-k+1 (eller Bk för den delen). Mängden kanter i grafen kan inte vara mera än (n-k+1) * B, eftersom varje nod har högst en kant per bokstav. 3-strängar kan fortsättningsvis visualiseras som en graf, vilket till slut leder till en n-sträng, vilket måste vara ordet vi söker efter.
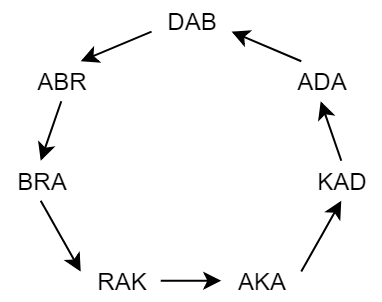
Notera att grafen för alla 3-strängar i ”abrakadabra” har blivit en stor ögla. I detta fall kan man gissa sig fram till lösningen genom att välja en nod som startpunkt, och sedan åka ett varv runt. I detta fall får man till näst gissningarna ”abrakadab”, ”brakadabr” och ”rakadabra”. Dessa skapar en simpel graf på 3 noder som sedan leder till ordet vi letade efter, ”abrakadabra”
Värsta möjliga antalet gissningar för ord blir till sist:
B/2 + B2/2 + (n-1) B + (n-2) B + … + 1 B = B/2 + B2/2 + n2B/2 – nB/2
vilket vi kan avrunda glatt till n2B. I verkligheten krävs det mycket mindre arbete, eftersom grafen som bildas snabbt blir en ögla (”abrakadabra” krävde 45 + B gissningar, och en 137 karaktär lång meddelande krävde ~2100 + B gissningar). Att räkna ut det praktiska tidskravet av den presenterade algoritmen lämnar jag som läxa för läsaren.
PS. Fresh Prince of Bel-Air theme orden (1788 tecken) löses på 31446 gissningar.