Det är dags för en till ramble om matematisk logik.
Observera följande påstående:
”I varje bar finns en person så att om han dricker, dricker alla.”

Är påståendet sant eller falskt? Intuitivt låter det ju som total nonsense, men meningen kan granskas exakt med hjälp av predikatlogik.

Då vi betecknar personer i baren med x och y, fås följande symboliska form:

Kort förklaring:

• betyder ”det existerar x så att…”
• betyder ”för alla y gäller…”
• innebär ”x dricker”
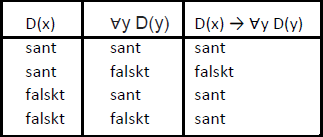
• är en implikation, som har följande sanningstabell:

Två distinkta situationer gäller nu för baren:
Om alla i baren dricker, kan vi välja vilken som helst person . Då är en sådan person, att om han dricker, dricker alla.
Om det föregående inte gäller, finns det en person i baren som inte dricker. Nu är båda påståendena och falska, så enligt sanningstabellen ovan är implikationen sann.

Tolkat i predikatlogik är alltså påståendet alltid sant, dvs. vi har en tautologi. Detta kan även verifieras exakt t.ex. med Tarskis sanningsdefinition.

Men beakta nu följande situation med tre personer på en bar:

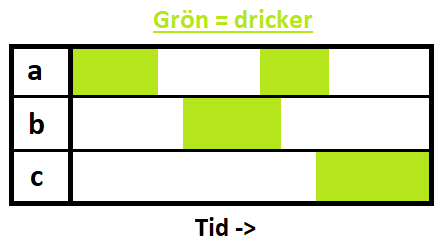
Alla personerna dricker vid något skede, men ingen av dem får alla andra att dricka samtidigt. Nu verkar påståendet igen inte stämma, what gives?

Vad vi nyss har diskuterat är Drinker Paradox, som i själva verket inte är en paradox, men illustrerar hur matematisk logik inte alltid stämmer överens med naturligt språk. Skillnaden ligger i hur implikationer tolkas: i naturligt språk är en implikation inte meningsfull ifall premissen är falsk. Däremot har logikens s.k. materiella implikation ingen sådan begränsning: en levande person som påstår ”om jag är död lever jag förevigt” skulle tala sanning enligt denna modell.

Då vi ännu återgår till baren och figuren ovan, märker vi att logik inte tar tidsdimensionen i beaktande. Påståendet gäller bara som en materiell implikation då en specifik tidpunkt fixeras. Detta är meningsfullt, eftersom kunder kan anlända till och lämna baren, och i synnerhet kan vi inte tala om drickande personer ifall baren är tom.

Den materiella implikationen är inte onödig eller meningslös inom matematik, men tolkat inom en vanlig mening kan vi formulera väldigt underhållande ”sanna” påståenden. Om du vill hitta på egna: ersätt och med andra personer eller föremål, och med någon annan egenskap än ”dricker”, så får du t.ex.

”I varje godispåse finns en karamell så att om den är choklad, 
är alla karameller choklad.”

”I varje ämnesförening finns en person så att om han är vegan, 
är alla veganer.”

”I varje människokropp finns ett ben så att om det benet bryts, 
bryts alla ben.”