Slutet av september är här vilket betyder att tillkännagivandena av de olika nobelpriserna ligger precis kring hörnet. Från och med nästa vecka (2.-9.10.2023), börjandes från nobelpriset i fysiologi eller medicin, kommer vi få ta del av genialiska upptäckter gjorda av världens forskningselit. För att bli del av denna elit krävs ofta en livstids erfarenhet och tiotals år inom forskningsväsendet. Om ingen annan, så förstår dessa garvade forskare att det inte alltid kommer gå riktigt som man tänkt sig i labbet. Därför är det mycket viktigt att lyssna och ta in sagan som experimentet berättar i stället för att kasta bort kolven när lösningen i den blir gul i stället för blå som den borde bli. Det finns en stor mängd forskare i världen som har just denna förmåga att tolka avvikelser, och det är mycket sannolikt att någon av dessa framstående forskare kommer bli belönad för sin berättarkonst. Själv väntar jag på dessa tillkännagivanden, speciellt priset för kemi (bild 1), med spänning och förväntning. För att få er på samma stämningsfrekvens tänkte jag berätta om några misstag som ändrat på världen och belönat forskare med nobelpris.
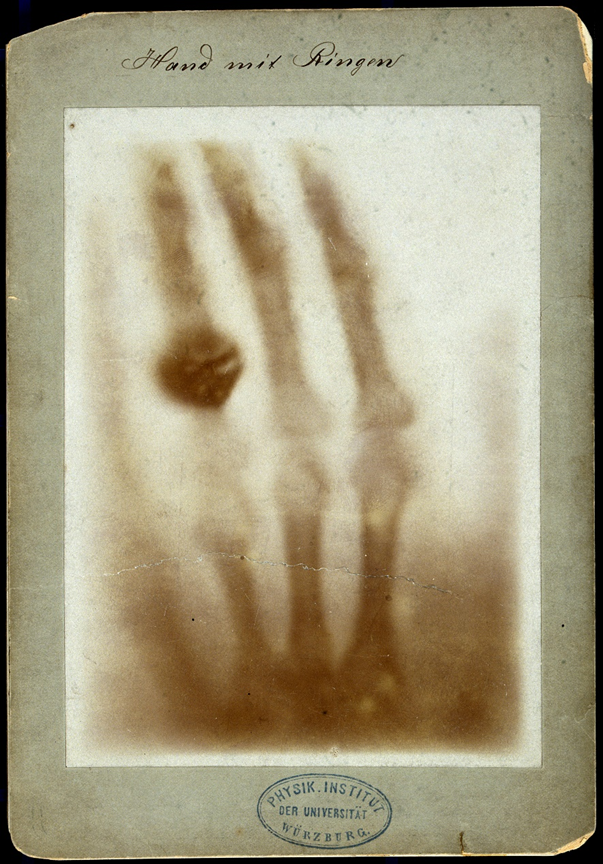
Wilhelm Röntgen var en tysk fysiker som först studerade gasers specifika värmekapacitet och kristallers värmeledningsförmåga. Senare övergick han till att studera ett fenomen där elström leds genom gaser vid lågt tryck. Fenomenet var i sig inte okänt och en mängd forskare hade studerat fenomenet före honom, bland annat William Crookes, som uppfann Crookesröret. Crookes och andra forskare använde ifrågavarande rör för att studera strålning och luminescens. Crookes märkte i ett experiment med fotografiska plåtar, att plåtarna blev dimmiga, men bekymrade sig inte med att undersöka orsaken. Även en forskare vid namn Philipp Lenard märkte att en fotografisk plåt fluorescerade i närheten av röret, men inte han heller undersökte denna orsak. Däremot var Röntgens sinne snäppet skarpare. Röntgen omslöt Crookesröret med en tjock svart kartong för att utesluta allt ljus, och märkte hur en liknande fotografisk plåt började lysa på långt avstånd. Dessutom märkte han via projektionen på den fotografiska plåten hur vissa objekt, bland annat hans frus hand (bild 2), hade olika transparens till strålningen. Röntgen förstod att detta måste handla om en ny sorts strålning. Ingen av er kan säkert gissa vad denna nyfunna strålning kom att heta!
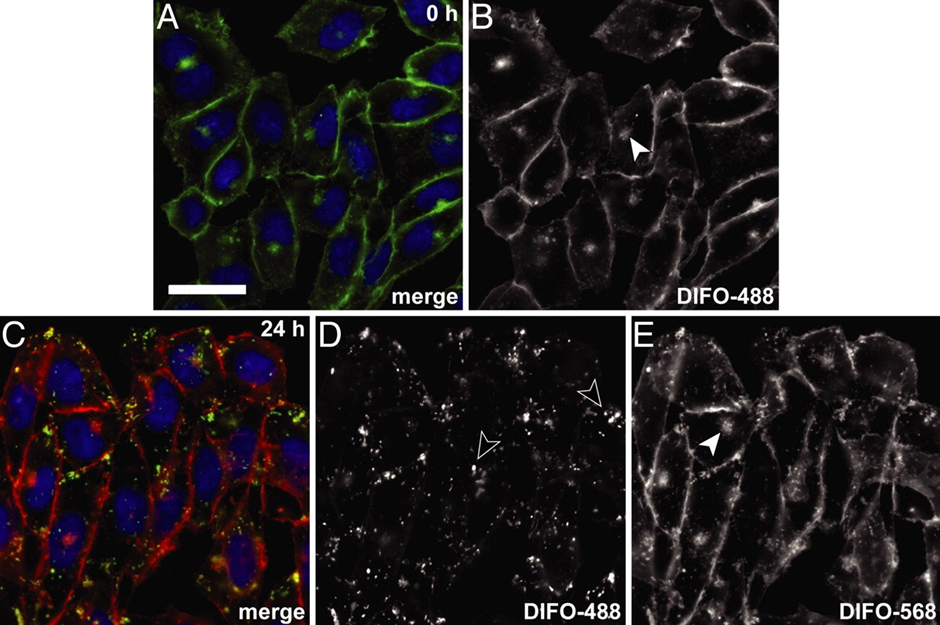
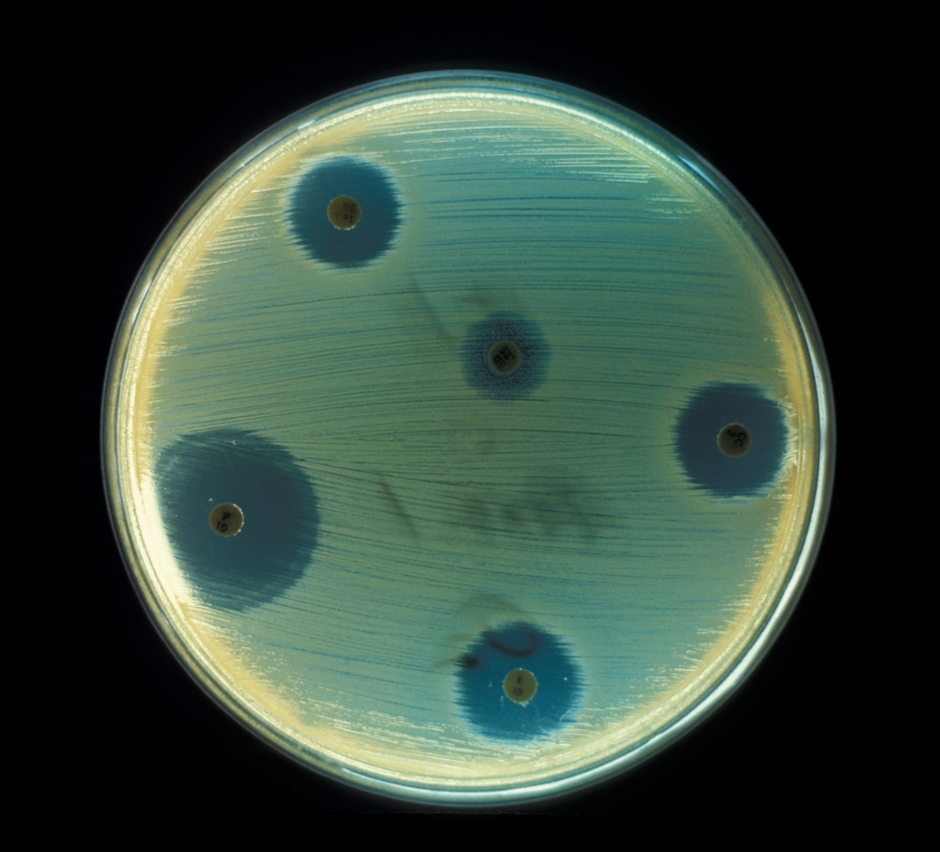
Även Alexander Fleming var en forskare med skarpt sinne, dock var han lite slarvig emellanåt. Sommaren 1928, då Fleming arbetade med influensakulturer, glömde han skydda sina inokulerade plattor före sitt sommarlov. När Fleming återvände från semestern, märkte han att kulturerna hade kontaminerats med mögel. Detta var ju lite synd för experimentets del, men samtidigt gjorde han en världsändrande observation: han märkte att området kring mögelväxten var helt fritt från stafylokocker (bild 3). Fleming drog slutsatsen att möglet bildar en substans som är giftigt för stafylokockerna och kallade denna antibiotika för penicillin. Denna skarpa observation, eller från en annan synvinkel slarv, belönades med nobelpriset i fysiologi eller medicin 1945.
Ibland kan fortsatta studier av något avvikande även hindras av ett skarpt sinne. Detta var fallet för Louis Claude Cadet de Gassicourt, en fransk kemist som isolerade den första organometalliska föreningen, kakodyl, så tidigt som 1757. Även syntesen av kakodyl var ett misstag, men på grund av den starkt kvävande vitlökslukten som fäste sig vid allt tänkbart, ville Cadet inte undersöka substansen. Med eftertanke var detta också ett vist beslut, eftersom arsenikförgiftning kan ha digra följder. Dessutom skulle han i ett så tidigt skede av vetenskapens historia inte ha haft tillgång till metoder för att karakterisera denna förening, och därmed skulle inte ens en sylvass observationsförmåga ha varit tillräckligt.
Följden var att organometallisk kemi såg världens ljus först kring det tjugonde århundrandet i och med syntesen och karakteriseringen av Zeises salt. Efter detta gjordes många viktiga upptäckter relaterade till organometallisk kemi, som senare belönats med flertalet nobelpris. Bland dessa finner vi grignardreaktionen som de flesta kemister utfört under sin karriär, och Ziegler-Natta katalysatorer som används för att framställa den mest använda plasten polyeten. Detta betyder att varje gång du kommer hem från Alepan med plastpåse i hand, så bär du hem resultatet av ett nobelpris.
Från alla dessa exempel ser vi att flit inte alltid belönas, utan ibland är det ett skarpt sinne och rena slumpen som avgör. Som student med kalendern full av kurser och sitsar kan det vara svårt att hållas skarp, även efter flera muggar kaffe. Just detta kan ändå belöna dig, dock får du nog vänta på ditt nobelpris många år ännu. Oberoende kvarstår frågan: Är du tillräckligt slarvig för att förtjäna ett nobelpris? Detta får alla timmar av prokrastinering i kafferummet bestämma.
Källor
Serendipity, Discovery, and the Nobel Prizes in Science, Brian J. Miller 1998, Vanderbilt, hämtat från https://www.vanderbilt.edu/AnS/physics/brau/H182/Term%20Papers/Brian%20Miller.html, september 2023
Wilhelm Conrad Röntgen Biographical, NobelPrize.org, hämtat från https://www.nobelprize.org/prizes/physics/1901/rontgen/biographical/, september 2023
Definition, Importance and History of Organometallics, LibreTexts Chemistry, hämtat från https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Supplemental_Modules_and_Websites_(Inorganic_Chemistry)/Advanced_Inorganic_Chemistry_(Wikibook)/01%3A_Chapters/1.18%3A_Definition_Importance_and_History_of_Organometallics, september 2023
Cadet’s Fuming Arsenical Liquid and the Cacodyl Compounds of Bunsen, Seyferth, Organometallics 2001, 20, 8, 1488–1498
Serendipity and Scientific Discovery, Bosenman, Journal of Creative Behavior 1988, 22, 2, 132-138








