I vår nya fina Spektrakel-blogg kommer jag (och förhoppningsvis även andra) med slumpmässiga intervall att skriva artiklar om matematiska problem som jag tycker är intressanta. Denna del av bloggen har jag valt att kalla Matematikhörnan. Det första inlägget handlar om delbarhet.
Delbarhet är en grundläggande men viktig del av talteori. Detta inlägg går igenom grunderna med delbarhet och kongruenser, och i slutet presenteras några små resultat.
Obs! Ifall inte annat nämns, är alla tal i denna artikel heltal.
Definitioner och några enkla satser
Definition 1: Talet d delar talet n, om 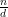 är ett heltal. Vi betecknar detta
är ett heltal. Vi betecknar detta  . Ifall d delar n kan vi alltså skriva
. Ifall d delar n kan vi alltså skriva  för något heltal k.
för något heltal k.
Definition 2: Vi säger att talen a och b är kongruenta modulo n, ifall 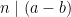 . Detta betecknas
. Detta betecknas  (mod n).
(mod n).
En observation: Ifall  , gäller
, gäller 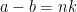 , dvs. differensen av a och b är en multipel av n.
, dvs. differensen av a och b är en multipel av n.
Sats 3: Om 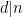 och
och 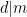 , så gäller för alla heltal a och b att
, så gäller för alla heltal a och b att 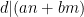 .
.
Bevis: Vi vet att  och
och  för några l och k, alltså gäller det att
för några l och k, alltså gäller det att 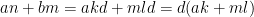 , dvs
, dvs 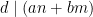 .
.
Sats 4: Ifall  (mod n) och
(mod n) och 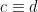 (mod n), så gäller
(mod n), så gäller 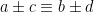 (mod n) och
(mod n) och 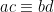 (mod n).
(mod n).
Bevis: Eftersom 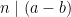 och
och 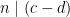 , gäller enligt föregående sats att
, gäller enligt föregående sats att 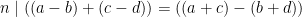 , och även
, och även 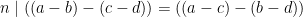 . Alltså gäller första påståendet.
. Alltså gäller första påståendet.
För att visa det andra påståendet räcker det att märka att enligt Sats 3 gäller det att 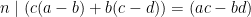 .
.
Av Sats 4 följer enkelt följande:
Följdsats 5: Om  (mod n), så gäller
(mod n), så gäller 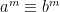 för alla positiva heltal m.
för alla positiva heltal m.
Några välkända delbarhetsresultat
Vi kan med hjälp av satserna ovan bevisa några praktiska resultat om delbarhet. Troligtvis vet vi alla från tidigare att ett tal är delbart med två om och endast om dess sista siffra är delbar med två, och att ett tal är delbart med fem om och endast om dess sista siffra är delbar med fem. Värför gäller då detta?
Som bekant kan vi skriva alla heltal k i formen 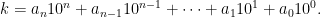
Eftersom 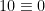 (mod 2) och
(mod 2) och 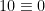 (mod 5), gäller alltså även att
(mod 5), gäller alltså även att 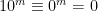 (mod 2) och (mod 5) för alla positiva m, alltså får vi att
(mod 2) och (mod 5) för alla positiva m, alltså får vi att
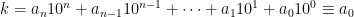 (mod 2) och (mod 5).
(mod 2) och (mod 5).
Delbarheten beror alltså endast på sista siffran.
Ett lite mindre trivialt, men ändå välbekant resultat är att ett tal är delbart med tre om och endast om dess siffersumma är delbar med tre: Eftersom  (mod 3), är även
(mod 3), är även 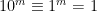 (mod 3), och därmed följer
(mod 3), och därmed följer
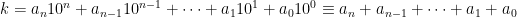 (mod 3),
(mod 3),
Exempel: 432 är delbart med tre, eftersom 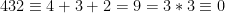 (mod 3).
(mod 3).
För stora tal kan metoden användas flera gånger, dvs. om siffersumman blir så stor att man inte direkt ser om den är delbar med tre, kan man beräkna siffersummans siffersumma och kontrollera om den är delbar med tre.
Vi märker också att eftersom  (mod 9), kan vi använda samma metod för att bestämma delbarhet med nio.
(mod 9), kan vi använda samma metod för att bestämma delbarhet med nio.
Fler delbarhetsresultat
Till näst undersöker vi delbarhet med 11. Eftersom 10 = 11 – 1, gäller  (mod 11). Därmed är
(mod 11). Därmed är 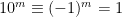 (mod 11) om m är jämnt och
(mod 11) om m är jämnt och 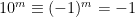 (mod 11) om m är udda. Då gäller alltså för talet k att
(mod 11) om m är udda. Då gäller alltså för talet k att
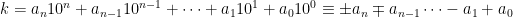 (mod 11),
(mod 11),
var tecknet på 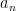 beror på om n är udda eller jämnt.
beror på om n är udda eller jämnt.
Exempel: 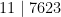 , eftersom
, eftersom 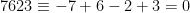 (mod 11).
(mod 11).
Exempel: 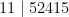 , eftersom
, eftersom 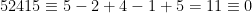 (mod 11).
(mod 11).
Exempel: 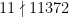 , eftersom
, eftersom 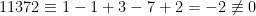 (mod 11).
(mod 11).
Vi kan alltså bestämma delbarheten genom att multiplicera siffrorna i talet med antingen talet 1 eller -1 och sedan summera dem.
Sekvensen för vilket tal vi skall multiplicera med vilken siffra är för talet 11 alltså (ifall vi börjar från den minst betydande siffran) 1, -1, 1, -1 osv.
Från våra tidigare resultat får vi även sekvenserna för följande tal:
- 2: 1, 0, 0, 0…
- 3: 1, 1, 1, 1…
- 5: 1, 0, 0, 0…
- 9: 1, 1, 1, 1…
- 11: 1, -1, 1, -1…
Läsaren har säkert redan märkt att vi hoppat över ett primtal, nämligen talet 7. Ifall vi beräknar sekvensen för talet 7, kan vi ganska enkelt med huvudräkning bestämma om ett tal mindre än 169 är ett primtal, eftersom då är dess kvadratrot mindre än 13, och då måste (minst) en av primtalsfaktorerna vara mindre än 13.
Vilken sekvens hittar vi alltså för sjuan?
Första talet i sekvensen är naturligtvis 1, eftersom 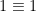 (mod n) för alla n.
(mod n) för alla n.
De övriga talen i sekvensen fås enligt följande:
$latex \begin{array}{ll}
10 \equiv 3\\
10^2 \equiv 3*3 = 9 \equiv 2\\
10^3 \equiv 3*2 = 6 \equiv -1\\
10^4 \equiv 3*(-1) = -3\\
10^5 \equiv 3*(-3) = -9 \equiv -2\\
10^6 \equiv (-1)^2 = 1
\end{array}$ (mod 7)
Vi ser nu att  (mod 7), och därmed kommer sekvensen att upprepa sig. Vi kan alltså fylla på vår lista:
(mod 7), och därmed kommer sekvensen att upprepa sig. Vi kan alltså fylla på vår lista:
- 2: 1, 0, 0, 0, 0, 0…
- 3: 1, 1, 1, 1, 1, 1…
- 5: 1, 0, 0, 0, 0, 0…
- 7: 1, 3, 2, -1, -3, -2…
- 9: 1, 1, 1, 1, 1, 1…
- 11: 1, -1, 1, -1, 1, -1…
Vi har nu räknat ut delbarhetssekvenserna för vissa tal, varav alla har en viss period varefter sekvensen upprepar sig. Kommer då sekvensen för alla naturliga tal att ha en ändlig period, dvs. har alla tal en sekvens som i något skede börjar upprepa sig? Denna fråga undersökes i min nästa artikel i Matematikhörnan.
Sebbe
Referenser:
Anne-Maria Ernvall-Hytönen: Elementär talteori. Föreläsningsanteckningar, Helsingfors universitet, 2013.









