Varning!
Följande artikel innehåller grunden för lösningarna till och för alla problem i världen.
Läs på egen risk!
Som spelmånadens sista spelartikel talar vi om… SPEL! Men denna gång i form av en liten introduktion av spelteori.
Vad går spelteori då ut på? Det handlar ganska långt om att man i olika spel söker fram vad är det rationellt sett bästa draget. Spelen utgår alltså från att spelarna är rationella och inte låter “känslor” eller “moral” påverka deras drag. Man är ute efter att maximera ens egen vinst och inget mer. Vi tar och kollar på ett trivialt spel som exempel:
Anta att en studerande, vars favoritmat är pizza, är hungrig och har nyligen inskaffat sin favoriträtt. Låt pizzan vara godtyckligt god och mättande. Studeranden har nu två val: att äta pizzan eller inte äta den. Matrisen för detta spel skulle se ut på följande vis:
Det självklara valet skulle nu vara (rationella som vi är) att äta pizzan. Att låta bli att äta pizzan ger inget bättre jämfört med att äta den.
Hänger du med såhär långt? Då går vi vidare till spel med två spelare:
Anta att två studiekamrater råkar se varandra vid Kampen på ett avstånd som överskrider den socialt acceptabla hälsningen. Om en av dem hälsar, så hälsar den andra nog tillbaka och saken är biff. Om ingendera hälsar börjar båda fundera på saken, vilket känns pinsamt. Matrisen för detta spel skulle se ut som följande:
Vad är det bästa draget? Rationella som vi är, så vill vi inte skapa friktion mellan våra vänskapsband, så det självklara draget skulle nu vara att hälsa. Det räcker med att ena börjar hälsningen, men eftersom en hälsning inte kräver mycket ansträngning, så kan man lika bra själv hälsa genast.
Förrän vi går vidare till nästa spel, så tar vi en tillbakablick på spelet ovan. I spelet är det relativt enkelt att se vad det bästa valet är, men vad om det inte skulle vara lika klart? Då kan vi använda oss av det fina verktyget som kallas matematik! Vi kan ge resultaten olika värden beroende på hur bra de är och från dessa värden kan vi sedan räkna ut den bästa strategin. I spelteorin används benämningen Nash equilibrium (Nash jämnviktsläge, eller förkortat bara Nash) för de bästa strategiparen och dessa kan räknas enligt följande:
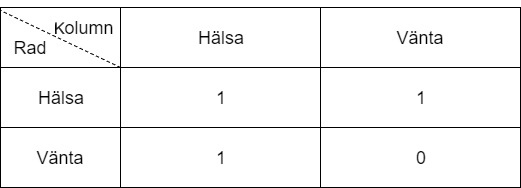
Vi kollar på hälsningsmatrisen pånytt, men denna gång ur matematisk synvinkel med värdena 0 och 1 som resultat.
Låt oss säga att vi nu spelar som radspelaren. Nu kan vi från matrisen se att om kolumnspelaren väljer att Hälsa får vi i vilket fall som helst resultatet 1. Alltså är båda dragen lika värda för tillfället. Till näst kollar vi på vad som händer om kolumnspelaren väljer att Vänta. Nu ser vi att draget Hälsa ger resultatet 1, medan Vänta ger resultatet 0. Eftersom 1 > 0 vill vi då hellre välja att Hälsa. Därmed lönar det sig alltid som radspelare att Hälsa. Spelet är symmetriskt, så då vi undersöker kolumnspelaren kommer vi också fram till att det alltid lönar sig för kolumnspelaren att Hälsa. Detta ger oss att vårt Nash är (Hälsa, Hälsa), eftersom det lönar sig för både och att Hälsa.
So far so good. Nu när du fått en inblick till spelmatriser och deras lösningar så tar vi en titt på svårare spel. Till näst använder vi oss av spelteori för att komma fram till den populationsdynamiskt sett evolutionärt stabilaste och optimalaste dejtningsstrategin (Varning! Har inte testats i praktiken (med framgång)).
Vi börjar med att kolla på dejtningsspelet.
I dejtningsspelet finns det två strategier, att sikta på en längre dejtningsperiod där man bygger upp ett romantiskt förhållande under en längre tid (med långa tysta promenader runt Kaisaniemi <3) eller sen kan man gå rakt på sak och genast hoppa i sängen med den andra. Om spelarna har olika dejtningsstrategier tar tålamodet slut för den som valt en Kort strategi. Förhållandet går ingen vart och i så fall har båda slösat sin tid.
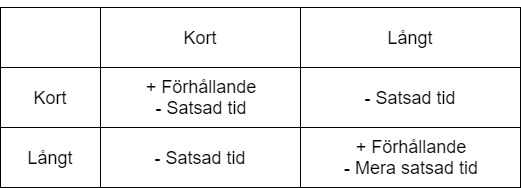
Alltså får vi följande matris:
Om man är fullkomligt rationell väljer man förstås den kortsiktiga strategin, eftersom tidsförlusterna är då mindre och man får lika mycket ut av förhållandet såsom man skulle få vid långtidsstrategin. Genom att ge matematiska värden för dessa, så har vi matematiskt bevisat att det lönar sig att dejta kortsiktigt. (Inte riktigt sant, eftersom både (Kort, Kort) och (Långt, Långt) kan vara Nash, beroende på hur mycket ett förhållande är värt jämfört med den satsade tiden, men vi håller oss till en ensidig åsikt för artikelns skull.)
Till näst ser vi på uppfostringsspelet.
I detta spel har spelarna *erhem* kopulerat och tillsammans fått en avkomma. Misstag eller inte, alternativen för båda spelare är att Stanna med sin avkomma eller Rymma iväg. Om båda spelare väljer Stanna, så delar de på tiden att uppfostra avkomman, medan om båda väljer Rymma, så kommer Socialen och för bort den (till en onämnd plats).
Vid fallet att spelarna väljer olika, så kommer den som valt att Stanna att ta fullt ansvar för avkomman, medan den som valt Rymma går vidare i livet nöjd av att ha (re)producerat en avkomma.
Notera att matrisen inte längre är symmetrisk! Eftersom det är skillnad vid (Rymma, Stanna) och (Stanna, Rymma), så kollar vi i denna matris specifikt alltså på radspelarens resultat!
Här märker vi att den bästa strategin beror på hur mycket man rationellt sett värderar Avkomman jämfört med ansträngningen av Uppfostran. Beroende på dessa parametrar, så kan vi få som Nash antingen (Stanna, Stanna) eller (Rymma, Rymma).
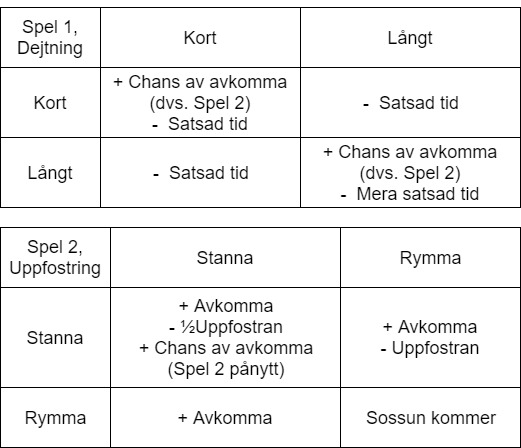
Men vad om man vill kolla på flera saker samtidigt och inte bara en sak i taget? Spelteori har lösningen även för det! Ett spel kan innehålla flera faser, där faserna är mindre enskilda spel. Exempelvis kan vi kombinera de två spelen ovan för att få följande spel:
Lösningen för dejtningsmatrisen är nu beroende av uppfostringsmatrisen, så vi måste lösa den först. Med vidare matematisk bollning (vilket ni kan bekanta er på i “Evolution and the Theory of Games”-kursens material) får vi till sist att de rationellt sett bästa strategierna är (Kort och Stanna) och (Kort och Rymma). Detta gäller för nästan alla parametrar (dvs. värderingarna på Avkomman med mera). I vissa fall är också (Lång och Stanna) lönsam, men vi kan alla hålla med om att det är onödigt att sätta för mycket tid på romantik!
Slutresultatet är att ifall alla skulle vara rationella istället för att bry sig om onödiga saker som känslor och annat tjafs, så skulle alla vara i korta förhållanden och sedan se hur mycket man bryr sig om avkomman. Så säger spelteorin… och matematiken ljuger aldrig!
– Team WaPaa