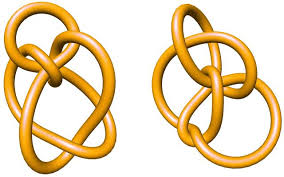Etikettarkiv: Matematik

2015, Blogg

Knutar

10 november, 2015 Joar Jensén Lämna en kommentar

Knutar och knopar är användbara i alla möjliga sammanhang, till exempel då man förtöjer båtar eller knyter skor. Det finns alla möjliga knopar för olika ändamål och det skulle ju förstås vara intressant att veta hur många knopar det egentligen finns. Inom topologin klassificerar man knopar med hjälp av dess symmetri och antalet gånger repet korsar sig själv. Till skillnad från knutar man använder i vardagen, så är repändarna inom knutteori förenade så att knuten inte går att knyta upp. Den enda icke-knuten är en cirkel där repet inte korsar sig själv en enda gång. Däremot finns det en hel del icke-knutar som är så ”ihoptvinnade” att man inte direkt ser att det inte är en egentlig knut.

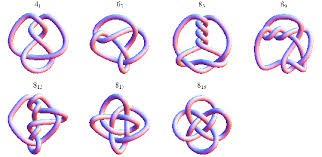
Olika knutar och knutkonfigurationer

Antalet olika knutar man för tillfället känner till:

Antalet ”korsningar” Antalet knutar
3 1
4 1
5 2
6 3
7 7
8 21
9 49
10 165
11 552
12 2176
13 9988
14 46 972
15 253 293
16 1 388 705

Två knutar är identiska om man kan manipulera den ena så att den blir likadan som den andra utan att klippa av repet. Däremot är det inte helt lätt att komma fram till vilka knutar som är identiska och vilka som är olika. År 1899 publicerade C. N. Little en lista på 43 olika knutar som alla hade tio ”korsningar”. Det visade sig först 75 år senare att det bland dessa 43 knutar fanns två stycken identiska knutar, nämligen knutarna 10_161 och 10_162. Det var juristen Kenneth Perko som genom att manipulera knutar gjorda av rep på sitt golv kom fram till att två av Littles knutar var identiska. De här två identiska knutarna kallas därför för Perkopar. Här nedan är knut 10_161 och 10_162, så du kan själv prova att lösa problemet.

Perkopar

I och med denna upptäckt märker man att det inte krävs att man är matematiker på heltid för att göra intressanta upptäckter inom matematik. Frågeställningen i sig är väldigt enkel; ”Är de här två knutarna identiska?”, men svaret kan vara mycket svårt att få fram. På grund av det här krävs det ändå inte så mycket matematisk kunskap för det här, utan man kan, så som Perko, bevisa svaret med hjälp av riktiga rep och knutar. Man måste bara vara tillräckligt intresserad och investerar lite tid i det hela.

Knutar är väldigt bekanta och vardagliga fenomen, som används i många former av handarbete, till exempel stickning, virkning och makramé. Forskningen inom knutteori handlar till stor del om knutgrupper och att klassificera knutar. Knutteorin har även kopplingar till matematiska metoder inom statistisk mekanik och kvantfältsteori. Dessutom kan knutteori användas för att förstå molekylers kiralitet och hur enzymer bearbetar DNA.

Som en äkta fysiker och experimentalist kännde jag mig förstås tvungen att knyta några egna knutar. Jag vågade mig ändå inte på att börja manipulera Perkos knutar, utan jag gjorde istället två stycken knutar med åtminstone 100 korsningar. De kan användas till exempelvis som nyckelringar.

2014, Blogg

Ren matematik, datamatematik och hur man kan lösa det olösliga

14 september, 2014 Spektraklet Lämna en kommentar

En betydande del av den nutida forskningen inom matematik använder datorer som hjälpmedel. Naturligtvis är användningen av datorer mest utspridd i tillämpad matematik och i statistik (bl.a. i form av Monte Carlo-metoder), men dataprogram kan även användas för att bevisa satser som känns väldigt teoretiska. Det mest välkända exemplet lär vara beviset på fyrfärgssatsen.

Datorer har dock ett antal begränsningar: man kan mekaniskt, genom att gå igenom fall ett för ett, bevisa något endast för ett ändligt antal fall. Beräkningar gjorda av en dator är dessutom inte exakta i alla fall. Detta beror på att det i de flesta fallen finns endast en begränsad mängd minne reserverat för decimaltal, och därmed tappar man i vissa fall precision då man utför beräkningar. Oftast är detta ej önskevärt, men i vissa specialfall kan man faktiskt utnyttja denna brist för att göra beräkningar som tekniskt sett inte borde vara möjliga!

Tänk dig att vi skulle i något sammanhang ha behov av en funktion som tar in två reella tal och ger som resultat dess summa, förutom om talen är lika. Ifall talen är lika ger den ut det ena av talen (vilket av dem spelar ingen roll eftersom de är lika). Uttryckt matematiskt är vi alltså intresserade av funktionen $f\colon \mathbb{R}^2 \rightarrow \mathbb{R}$ , där

$f(x, y) = x + y$ ifall $x \neq y$ , och
$f(x, y) = x$ ifall $x = y$ .

På en dator kan ovanstående konstruktion i vanliga fall lätt implementeras med hjälp av en if-sats, men låt oss nu anta att vi av någon orsak inte kan använda oss av konditionaler. Istället måste vi uttrycka ovanstående funktion med hjälp av endast de fyra grundräknesätten. Först skulle vi säkert försöka skapa en multiplikation med noll i något skede för att få en av termerna att försvinna i fallet där de båda är lika:

$x + (x-y)\cdot y \qquad \: (1)$ .

Detta fungerar ifall $x = y$ , men om $x \neq y$ får vi $x + xy - y^2$ , vilket vi inte ville. Vi borde alltså i fallet $x \neq y$ lyckas få den tillagda överloppstermen $x-y$ att försvinna. Ett sätt är att istället använda sig av formeln

$x + \frac{x-y}{x-y} \cdot y \qquad \: (2)$ .

Ifall $x \neq y$ , så ger ovanstående formel det korrekta resultatet $x + y$ . Tyvärr så fungerar den ej i fallet $x = y$ , eftersom vi då stöter på problemet att dividera med noll.

Eftersom de första, mest uppenbara försöken att skapa formeln misslyckades, kan det löna sig att fundera en stund över orsaken på varför vårt tillvägagångssätt ej fungerade. Vi märker att funktionen $f\colon \mathbb{R}^2 \rightarrow \mathbb{R}$ är definierad för alla par av reella tal. Därmed kan vi inte i något skede dela med ett uttryck som kan bli noll, eftersom vi då får till stånd ett par av reella tal där formeln ej är definierad.

Ifall vi undersöker funktionen $f$ närmare märker vi även att den inte är kontinuerlig i hela $\mathbb{R}^2$ . Problempunkterna är punkterna av typen $(a,a)$ där $a \neq 0$ . Om vi t.ex. slår fast x-koordinaten att vara 2, ser vi att det för gränsvärdena gäller att $\lim\limits_{y \to 2^{+}} f(2,y) = \lim\limits_{y \to 2^{-}} f(2,y) = 4$ , men att $f(2,2) = 2$ . Vårt mål var att beskriva funktionen $f$ endast med hjälp av de fyra grundräknesätten. Det är välkänt att funktioner som är uppbyggda endast med hjälp av de fyra grundräknesätten är kontinuerliga i hela sin definitionsmängd. Därmed är det omöjligt att beskriva funktionen $f$ endast med hjälp av grundräknesätten eftersom funktionen inte är kontinuerlig!

Det verkar alltså som vi skulle ha kört fast, eftersom det rent matematiskt är omöjligt att lösa problemet, givet de verktyg vi har. Detta är dock ett av de fall där vi kan utnyttja de begränsningar som datorer ställer på beräkningar av decimaltal. I vanliga fall beskrivs decimaltal av en dator på följande sätt:

$signifikand \cdot bas^{exponent}$ .

Eftersom varje decimaltal ges en konstant mängd utrymme i datorns minne, finns det en gräns på storleken på signifikanden (dvs. hur många signifikanta siffror talet kan ha) och även en gräns på hur stor exponenten kan vara. Detta leder till att datorn kan representera tal som är nära noll mycket noggrant, medan precisionen (absolut sett) blir allt mindre ju större talet är. Ifall vi som exempel slår fast basen att vara $10$ och antalet signifikanta siffror att vara $10$ och jämför exponenterna $-20$ och $20$ , ser vi att vi kring talet $10^{-20}$ kan representera skillnader av storleksordningen $0.000000001 \cdot 10^{-20} = 10^{-11}$ , medan vi kring talet $10^{20}$ endast kan representera skillnader av storleksordningen $0.000000001 \cdot 10^{20} = 10^{11}$ ! Därmed om vi t.ex. skulle göra beräkningnen $10^{20} + 1$ skulle resultatet vara $10^{20}$ , eftersom vi ej kan representera tal så noggrant kring $10^{20}$ .

Hur kan vi då utnyttja detta fenomen för att lösa vårt ursprungliga problem? Vi hade tidigare skapat formeln $(2)$ , som fungerar bra förutom att vi kan tvingas dela med noll. För att undvika division med noll kan vi modifiera formeln på följande sätt:

$x + \frac{x-y}{(x-y) + \varepsilon} \cdot y \qquad \: (2′)$ ,

där $\varepsilon$ är ett till absolutbeloppet mycket litet positivt tal (storleken på talet beror på representationen av decimaltalen). Matematiskt sett gäller naturligtvis inte att $(x-y) + \varepsilon = x-y$ , men p.g.a. bristerna i decimaltalsberäkningen kommer likheten att gälla ifall $x$ och $y$ är olika och är tillräckligt stora. Kvoten $\frac{x-y}{(x-y) + \varepsilon}$ är alltså $1$ ifall $x \neq y$ , och därmed uppfyller formeln $(2′)$ kravet att $f(x,y) = x + y$ om $x \neq y$ .

Å andra sidan ifall $x = y$ , så är naturligtvis $x - y = 0$ och därmed är $0 + \varepsilon = \varepsilon$ , eftersom vi kan representera tal noggrant kring noll. Därmed undviker vi division med noll och kvoten $\frac{x-y}{(x-y) + \varepsilon}$ blir 0. Alltså gäller det för formeln $(2′)$ även att $f(x,y) = x$ ifall $x = y$ .

Vi har alltså lyckats trolla fram en formel som med hjälp av datorberäkningar löser ett matematiskt sett omöjligt problem. Dock har formeln sina begränsningar; t.ex. får talen $x$ och $y$ ej vara för små, för då skulle additionen av talet $\varepsilon$ påverka det slutliga resultatet som formeln $(2′)$ ger. I de flesta fallen är precisionsproblemen i decimaltalsräkningen något man försöker undvika (se t.ex. Wikipedia-artiklen om ämnet), men i vissa fall kan man faktiskt dra nytta av dem. Det är bra att komma ihåg att begränsningar som datorer ställer inte alltid är endast negativa; i vissa fall kan vi p.g.a. begränsningarna lösa problem som annars vore olösliga.

Jag vill till sist tacka Lasse för idén till artikeln! Den som är intresserad att lära sig mer om ämnet kan börja t.ex. med Wikipedia-sidan IEEE floating point.

Sebbe

2014, Blogg

Dörrkodsproblemet

6 maj, 2014 Joar Jensén Lämna en kommentar

En skrämmande tanke

Föreställ dig följande scenario: Du är på väg till århundradets fest som förstås ordnas i Majstranden. Då du sitter på bussen märker du att du har glömt telefonen hemma, men du låter inte en sådan liten motgång sänka humöret. När du äntligen anländer till Majstranden och skall slå in dörrkoden märker du att du inte kommer ihåg den! ”Inget problem”, tänker du, för någon måste ju snart komma ut och så kan du slinka in samtidigt. Efter att ingen setts till på en kvart fattar du plötsligt att alla andra redan måste vara på festen (det är ju århundradets fest vi talar om), så det är klart att ingen är på väg ut på länge!

”Ingen orsak att panikera”, tänker du, ”detta problem går nog att lösa”. Du samlar ihop allt vad du vet om problemet: koden är fyra siffror lång (för alla koder är ju det), och från manicken du slår in den på ser du att den kan bestå av siffror från 0 till 9. Du beräknar snabbt att det finns totalt $10^4 = 10000$ möjliga koder, så ifall du prövar dem alla, måste dörren öppnas förr eller senare. För inmatandet av alla koder måste du då slå in $4 \cdot 10000 = 40000$ siffror.

Dörrkod

Hmm…1234 kanske?

Efter att du funderat på problemet en stund till, så kommer ~~någon och öppnar dörren~~ du ihåg att någon sagt åt dig att dörrkodsläsare brukar fungera lite konstigt. De kräver nämligen inte att man håller en paus efter att man slagit in de fyra siffrorna förrän den kollar ifall koden är korrekt. För att dörren skall öppnas räcker det att man i något skede slår in de fyra korrekta siffrorna i rad. Det har alltså ingen skillnad fast man matar in felaktiga siffror i början så länge den korrekta koden slås in i något skede. Ifall du slår in fem siffror har du alltså matat in två olika fyrsiffriga koder! Den första består av siffrorna 1-4, och den andra av siffrorna 2-5.

Du fattar direkt att för att alla koder skall finnas någonstans i den sekvens du slår in, måste du knappast mata in 40000 siffror, eftersom koderna överlappar varandra. Vilken strategi skulle det löna sig att använda för att få inslaget alla koder med så få siffror som möjligt? Naturligtvis lönar det sig att undvika upprepning av koder, alltså vill du i varje skede slå in en sådan siffra som skapar en fyrsiffrig kod som du inte matat in tidigare.

Simplifikation av problemet

För att simplifiera problemet rycker vi oss för en stund bort från vårat scenario och funderar i stället på en dörrkodsläsare som endast har siffrorna 0 och 1 och kräver en tvåsiffrig kod. Det finns alltså $2^2 = 4$ olika koder, nämligen koderna $00$ , $01$ , $10$ och $11$ . I vilken ordning skulle man slå in siffror i detta fall för att med så liten möda som möjligt få upp dörren? En möjlighet är att slå in sekvensen $11001$ . Den innehåller alla koder:

11001
11001
11001
11001

Är det möjligt att hitta en kortare sekvens som innehåller alla koder? Genom att analysera listan ovan ser vi fort att det inte kan gå. För att visa detta, antag att $L$ är en sekvens av siffror 0 och 1. Ifall den innehåller alla fyra olika koder av längd två, måste var och en av koderna starta vid olikt index i sekvensen. Därmed kan den sista koden starta som tidigast vid index 4, och eftersom den är av längden två, måste sekvensen $L$ vara minst fem siffror lång. Detta betyder att är sekvensen $11001$ den kortaste möjliga lösningen. Dock finns det andra lösningar av längden fem också, t.ex. $00110$ .

Binär dörrkod

Dörrkodsläsare, modell datalog (Patent pending)

Hur skapades då sekvensen $11001$ ? En möjlig strategi är följande: börja med den största koden (i detta fall $11$ ), och välj sedan den lägsta möjliga siffran som skapar en ny kod till sekvensen, dvs. en kod som inte från tidigare finns i sekvensen. Ifall detta alltid lyckas, kommer vi att få till stånd en möjligtvis kort sekvens, eftersom den inte upprepar några koder.

Ifall vi använder denna strategi i vårt ursprungliga scenario, kommer vi att få till stånd en sekvens av längden $10^4 + (4-1) = 10003$ (börjandes med siffrorna $9999$ ) som innehåller alla koder, en klar förbättring till att vara tvungen att mata in 40000 siffror!

Det allmänna problemet

Den stora frågan är följande: Kan vi för alla kodlängder $k$ och sifferantal (dvs. baser) $b$ alltid skapa en sekvens som inte upprepar någon kod två gånger? Svaret är kanske aningen överraskande ja. Beviset i sin helhet, till vilket det finns en länk i slutet av artikeln, är lite för invecklat för att tas upp i denna artikel, men det bygger på följande observation: Antag för enkelhetens skull att vi vill skapa koder av längd 4 som består av siffrorna 0, 1, 2 och 3. Ifall vi har någon kod, t.ex. $0233$ , kan efter denna kod i sekvensen följa endast en kod som börjar med siffrorna $233$ och slutar med en av siffrorna 0, 1, 2 eller 3. Detta gör att sekvensen blir mycket symmetrisk, eftersom det efter någon av koderna $0233, 1233, 2233, 3233$ endast kan följa någon av koderna $2330, 2331, 2332, 2333$ .

Tillämpning till scenariot

Smart som du är kom du på denna lösning till problemet på säg…22 minuter. Du började sedan knacka in siffrorna, och eftersom du har ett utomordentligt minne kunde du hålla reda på vilka koder du redan slagit in. Efter en dryg timme lyckades du därmed få upp dörren, och kvällen var räddad. Snäll som du är skapade du åt dina vänner en textfil med den kod som behövs för att öppna vilken som helst dörr med fyrsiffrig kod i bas 10!

Till sist

Ett stort tack till Lasse och Jeremias för hjälpen med detta problem!

Den som är intresserad att läsa mera om dörrkodsproblemet kan ta en titt på följande text (på engelska):

The door code problem

Ifall du vill veta den sekvens (av längden 10003) som du säkert kommer in till Majstranden med, kan du skriva ut följande textfil:

Bas 10, kodlängd 4

Spektrum rfs medlemstidning