Etikettarkiv: Matematik

2018, Vecktraklet

Lustiga limerickar och vetenskaplig vers

Lämna en kommentar

Matematiska texter från antikens och medelålderns Indien hade en egendomlig struktur. För att hjälpa läsaren minnas dem framställdes problem och resultat ofta som vers. Till exempel Bakshali-manuskriptet är en sådan text.

I nutidens utbildning är poesi en form som används väldigt lite inom vetenskaplig utbildning. Trots det hittar man på nätet många matematiska verser, som människor skrivit för skojs skull eller för att minnas dem bättre. En särskilt minnesvärd versform är limericken, varav några presenteras till näst (i ökande svårighetsgrad):

”A dozen, a gross and a score
Plus three times the square root of four
Divided by seven
Plus five times eleven
Is nine squared and not a bit more”

Ramsan beskriver följande simpla uträkning:
\displaystyle\frac{12+144+20+3\sqrt{4}}{7}+(5\cdotp 11) = 9^2 + 0
Huruvida ramsan är användbar eller inte lämnas till läsarens beaktande. Till näst nåt en aning knepigare:

”The integral z squared dz
From one to the cube root of three
Times the cosine
Of three pi over nine
Is the log of the cube root of e”

Här beskrivs en annan identitet:

\displaystyle\int_{1}^{\sqrt[3]{3}}z^2dz \cdotp \cos{\left(\frac{3\pi}{9}\right)} = \ln{\left(\sqrt[3]{e}\right)}

Läsaren må påminnas att \cos{\left(\frac{3\pi}{9}\right)} = \frac{1}{2} och \ln{\left(\sqrt[3]{e}\right)} = \frac{1}{3}.
I allmänhet är de två föregående verserna skrivna mer för poesins skull, inte för innehållet. Till sist ett mer sofistikerat resultat:

”Take M a complete metric space
If nonempty, it’s always the case
That if f’s a contraction
Then under its action
Exactly one point stays in place”

Versen beskriver den s.k. Banachs fixpunktssatsen. Utan att överkomplicera: I ett fullständigt metriskt rum gäller att om på varandra följande punkter i en följd kommer godtyckligt nära varandra, så har också hela följden en gränspunkt den går mot. En kontraktion är en funktion som, givet två godtyckliga punkter, flyttar dem närmare varandra än de var förut.

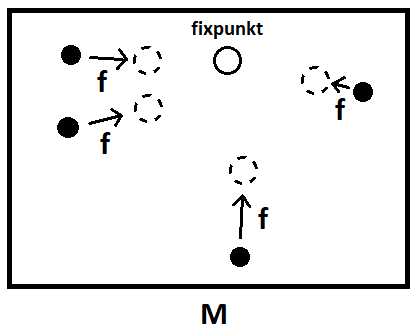
MS Paint-illustration av Banachs fixpunktssats

Satsen säger, att kontraktionen f har endast en unik fixpunkt, dvs. en punkt som inte rör sig då kontraktionen appliceras.

Limericken om Banachs fixpunktssats hjälpte mig faktiskt minnas satsen till provet i topologi. Poesi är ett kraftigt verktyg för att få något att fastna i huvudet, och jag skulle vilja se det användas oftare inom matematikutbildningen. Så länge innehållet är ändamålsenligt alltså; förvränger man ekvationer för att göra dem till limericks så gör man det nog mest för poesins skull.

 

2018, Vecktraklet

Kartor, grafer och kaffemuggar

Lämna en kommentar

De som har deltagit i gulisintagningen tidigare under hösten känner kanske till muggen ovan. Vid matematikpunkten på Wall Street Bar fick gulisarna till uppgift att med tusch koppla varje hus till varje enhet (el, vatten, gas) utan att förbindelserna korsar varandra. De fick med andra ord lösa det s.k. Three Utilities Problem. Om du vill fundera på problemet själv och undvika spoilers, gör det nu (Eller kolla på 3Blue1Browns video om temat, rekommenderas varmt).

Det väsentliga som gjorde uppgiften lösbar är att en mugg är (topologiskt sett) fundamentalt annorlunda än ett klot eller ett papper. Om man tänker sig att muggen är gjord av lera, kan man utan att bryta den eller slå nya hål forma om den till en donits. Med andra ord är kaffemuggen en torus, en sluten kropp med ett hål. Det visar sig att uppgiften är lösbar på en torus, men inte på ett klot eller ett papper!

 

Muggproblemet kan förvånansvärt nog ge oss insikt om ett helt annat problem: Om du har en karta där varje land är en sammanhängande region, hur många färger behöver du för att färglägga varje land utan att två grannländer får samma färg? Då kartan är ritad på ett papper eller en boll visar det sig att högst fyra färger behövs; resultatet är känt som Four color theorem.

Kartan över Frankrikes provinser behöver fyra färger

Men om kartan är ritad på en annan slags kropp, t.ex. en torus, räcker fyra färger till? För att förstå denna situation bättre söker vi ett ”renare” sätt att rita vår karta. Vi ersätter först varje region med en punkt. Sedan ritar vi streck mellan två punkter ifall de motsvarande regionerna gränsar till varandra. Det vi får är en graf: en samling noder (punkter) och kanter (streck) mellan dessa. I själva verket är det en planär graf, dvs. den kan ritas utan att två streck korsar varandra.

En karta och dess motsvarande graf

Det visar sig att varje karta motsvarar en planär graf och vice versa. Så istället för att granska kartor på en torus, kan vi kolla på planära grafer på en torus: Hur många färger behövs för att färglägga noderna så att två grannar inte får samma färg? Men här kommer insikten från muggproblemet in: Grafen som bildas i Three Utilities Problem är inte planär på ett papper (dvs två kanter måste korsa varandra) men den är planär på en torus. Det betyder att mängden av planära grafer på en torus är fundamentalt större!

Kan vi alltså hitta en graf som kräver mer än fyra färger? Grafen i muggproblemet kan färgas med endast två färger. Men t.ex. den kompletta grafen K5 kräver 5 färger och kan ritas på en kaffemugg utan att två kanter korsar varandra.

K5 ritad på en kaffemugg utan att två kanter korsar

Och vad är det högsta antalet färger vi kan behöva?
https://mathsgear.co.uk/products/7-colour-torus-mug

Det mest spännande inom matematiken är då två koncept som verkar mycket annorlunda egentligen är nära sammankopplade. Många situationer där vi beaktar föremål (länder) och förbindelser mellan dem (gränser) kan uttryckas med hjälp av grafteori. Men en grafs egenskaper hänger inte bara på grafen själv, utan också på kroppen den ritas på. Kaffemuggen är ett intressant topologiskt föremål, inte bara en pryl för att hälla i sig kaffe.

2018, Vecktraklet

Det absolut simplaste beviset att √2 är irrationellt

Lämna en kommentar

Har du någonsin läst standardbeviset för att √2 är irrationellt och tänkt något av följande?
– ”Usch, delbarhet”,
– ”Fy, motantaganden”, eller
– ”Det här beviset var helt för kort!”
Worry not! Här delar jag med mig mitt favoritbevis, som är så självklart och trivialt att till och med humanister kunde uppskatta dess skönhet!

Vi påminner oss ännu om att ett rationellt tal kan skrivas i formen \frac{a}{b}, där a och b är heltal och b ≠ 0. Ett irrationellt tal kan alltså inte skrivas på detta vis.

Påstående:

√2 är irrationellt.

Bevis:

Vi undersöker talföljder (a_n)_{n \geq 0}  med kraven
A) a_n är rationellt för alla n \geq 0
B) a_{n+1} = 2a_n^2 - 1 för alla n \geq 0
C) a_i = a_j för något i \neq j

Det visar sig att det finns ett ändligt antal talföljder som uppfyller dessa krav. Vi kan i själva verket lista upp dem alla.

Om |a_0| > 1 följer det från krav B att talföljden är strängt växande, dvs inget värde upprepas och krav C uppfylls inte. Vi kan alltså anta |a_0| \leq 1

Nu kan man substituera a_0 = \cos{t} för något t \in [0, \pi]. Detta kommer att ge oss en icke- rekursiv formel för talföljden.
Låt oss visa med induktion att a_n = \cos(2^nt) för alla n \geq 0.

Grundsteg:
a_0 = \cos{t} = \cos{(2^0t)}

Induktionssteg:
Med hjälp av formeln för dubbla vinklar, \cos{(2x)} = 2\cos^2{x} - 1,
får vi
a_n = \cos{(2^nt)} \implies a_{n+1} = 2a_n^2 - 1 = 2\cos^2{(2^nt)} - 1 = \cos{(2^{n+1}t)}

Påståendet a_n = \cos(2^nt) gäller alltså för alla n \geq 0.
Nu gäller det att hitta passliga värden på t \in [0, \pi] så att a_n = \cos{(2^nt)} är rationellt för alla a_n \geq 0 (krav A). I själva verket räcker det, att \cos{t} är rationellt, eftersom (”selvästi nähdään”) då är också \cos{(2t)}, \cos{(4t)}, \cos{(8t)} \dots rationella enligt formeln för dubbla vinklar.

För att krav C ska hålla, måste
\cos{(2^it)} = \cos{(2^jt)} för något i \neq j

\implies 2^it = \pm 2^jt + 2k\pi, k \in \mathbb{Z} \\ \implies t = \frac{2k}{2^i \pm 2^j}\pi

där täljaren och nämnaren är heltal och nämaren är olika noll.
Talet t måste alltså vara en rationell multipel av pi!

Nu finns ett användbart resultat, Niven’s Theorem, som säger att de enda rationella multiplarna av pi inom [0, \frac{\pi}{2}] vars cosinus också är rationellt är 0,  \frac{\pi}{3}  och  \frac{\pi}{2}. Satsens bevis använder sig lyckligtvis inte av talets √2 irrationalitet.

Med Niven’s Theorem och några trigonometriska identiteter får vi att t \in \{0, \frac{\pi}{3}, \frac{\pi}{2}, \frac{2\pi}{3}, \pi \}, varav följer a_0 \in \{1, \frac{1}{2}, 0, -\frac{1}{2}, -1 \}

Alla följder som uppfyller kraven A, B och C är alltså:
1, 1, 1, 1, 1, \dots
\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, \dots
0, -1, 1, 1, 1, \dots
-\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, \dots
-1, 1, 1, 1, 1, \dots

Men nu märker vi ju, att talföljden
\frac{1}{\sqrt{2}}, 0, -1, 1, 1, \dots
uppfyller kraven B och C, men hittas inte på vår lista. Då måste krav A gå fel, och eftersom 0, -1 och 1 tydligt är rationella tal, måste
\frac{1}{\sqrt{2}} och därmed  \sqrt{2} vara irrationellt, Q.E.D.

Funderingar

Det här beviset är ett gott exempel på hur samma matematiska påstående ofta kan bevisas på många olika sätt. Standardbeviset påminner mest om talteori, ofta kallad heltalens matematik. Beviset ovan använder sig mer av algebra (reella tal och deras räkneregler) och analys (förändringens matematik, dvs. talföljder, derivator…).

Ifall du läser detta stycke och inte har läst beviset, så gör det inte nåt. Alla är inte intresserade av matematik och ska inte heller behöva vara det. Men på samma sätt som en poet gillar att skriva och läsa dikter kan en matematiker bli riktigt begeistrad av ett vackert bevis. Det är alltid bra att ha ett öppet sinne för andras intressen, även om man inte vet vad de talar om. Då kanske det är dags för mig att plocka ner diktboken från hyllan…