Har du någonsin läst standardbeviset för att √2 är irrationellt och tänkt något av följande?
– ”Usch, delbarhet”,
– ”Fy, motantaganden”, eller
– ”Det här beviset var helt för kort!”
Worry not! Här delar jag med mig mitt favoritbevis, som är så självklart och trivialt att till och med humanister kunde uppskatta dess skönhet!
Vi påminner oss ännu om att ett rationellt tal kan skrivas i formen  , där a och b är heltal och b ≠ 0. Ett irrationellt tal kan alltså inte skrivas på detta vis.
, där a och b är heltal och b ≠ 0. Ett irrationellt tal kan alltså inte skrivas på detta vis.
Påstående:
√2 är irrationellt.
Bevis:
Vi undersöker talföljder  med kraven
med kraven
A) 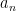 är rationellt för alla
är rationellt för alla 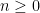
B)  för alla
för alla 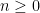
C)  för något
för något 
Det visar sig att det finns ett ändligt antal talföljder som uppfyller dessa krav. Vi kan i själva verket lista upp dem alla.

Om  följer det från krav B att talföljden är strängt växande, dvs inget värde upprepas och krav C uppfylls inte. Vi kan alltså anta
följer det från krav B att talföljden är strängt växande, dvs inget värde upprepas och krav C uppfylls inte. Vi kan alltså anta 
Nu kan man substituera  för något
för något ![t \in [0, \pi] t \in [0, \pi]](http://s0.wp.com/latex.php?latex=t+%5Cin+%5B0%2C+%5Cpi%5D&bg=ffffff&fg=000000&s=0) . Detta kommer att ge oss en icke- rekursiv formel för talföljden.
. Detta kommer att ge oss en icke- rekursiv formel för talföljden.
Låt oss visa med induktion att  för alla
för alla 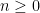 .
.
Grundsteg:
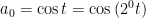
Induktionssteg:
Med hjälp av formeln för dubbla vinklar,  ,
,
får vi

Påståendet  gäller alltså för alla
gäller alltså för alla 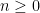 .
.
Nu gäller det att hitta passliga värden på ![t \in [0, \pi] t \in [0, \pi]](http://s0.wp.com/latex.php?latex=t+%5Cin+%5B0%2C+%5Cpi%5D&bg=ffffff&fg=000000&s=0) så att
så att  är rationellt för alla
är rationellt för alla  (krav A). I själva verket räcker det, att
(krav A). I själva verket räcker det, att 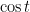 är rationellt, eftersom (”selvästi nähdään”) då är också
är rationellt, eftersom (”selvästi nähdään”) då är också 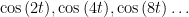 rationella enligt formeln för dubbla vinklar.
rationella enligt formeln för dubbla vinklar.
För att krav C ska hålla, måste
 för något
för något 

där täljaren och nämnaren är heltal och nämaren är olika noll.
Talet t måste alltså vara en rationell multipel av pi!
Nu finns ett användbart resultat, Niven’s Theorem, som säger att de enda rationella multiplarna av pi inom ![[0, \frac{\pi}{2}] [0, \frac{\pi}{2}]](http://s0.wp.com/latex.php?latex=%5B0%2C+%5Cfrac%7B%5Cpi%7D%7B2%7D%5D&bg=ffffff&fg=000000&s=0) vars cosinus också är rationellt är 0,
vars cosinus också är rationellt är 0, 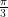 och
och  . Satsens bevis använder sig lyckligtvis inte av talets √2 irrationalitet.
. Satsens bevis använder sig lyckligtvis inte av talets √2 irrationalitet.
Med Niven’s Theorem och några trigonometriska identiteter får vi att  , varav följer
, varav följer 

Alla följder som uppfyller kraven A, B och C är alltså:
1, 1, 1, 1, 1, 
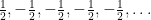
0, -1, 1, 1, 1, 

-1, 1, 1, 1, 1, 
Men nu märker vi ju, att talföljden

uppfyller kraven B och C, men hittas inte på vår lista. Då måste krav A gå fel, och eftersom 0, -1 och 1 tydligt är rationella tal, måste
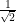 och därmed
och därmed  vara irrationellt, Q.E.D.
vara irrationellt, Q.E.D.
Funderingar
Det här beviset är ett gott exempel på hur samma matematiska påstående ofta kan bevisas på många olika sätt. Standardbeviset påminner mest om talteori, ofta kallad heltalens matematik. Beviset ovan använder sig mer av algebra (reella tal och deras räkneregler) och analys (förändringens matematik, dvs. talföljder, derivator…).
Ifall du läser detta stycke och inte har läst beviset, så gör det inte nåt. Alla är inte intresserade av matematik och ska inte heller behöva vara det. Men på samma sätt som en poet gillar att skriva och läsa dikter kan en matematiker bli riktigt begeistrad av ett vackert bevis. Det är alltid bra att ha ett öppet sinne för andras intressen, även om man inte vet vad de talar om. Då kanske det är dags för mig att plocka ner diktboken från hyllan…