Kategoriarkiv: 2018

Texter från 2018

2018, Vecktraklet

Kartor, grafer och kaffemuggar

Lämna en kommentar

De som har deltagit i gulisintagningen tidigare under hösten känner kanske till muggen ovan. Vid matematikpunkten på Wall Street Bar fick gulisarna till uppgift att med tusch koppla varje hus till varje enhet (el, vatten, gas) utan att förbindelserna korsar varandra. De fick med andra ord lösa det s.k. Three Utilities Problem. Om du vill fundera på problemet själv och undvika spoilers, gör det nu (Eller kolla på 3Blue1Browns video om temat, rekommenderas varmt).

Det väsentliga som gjorde uppgiften lösbar är att en mugg är (topologiskt sett) fundamentalt annorlunda än ett klot eller ett papper. Om man tänker sig att muggen är gjord av lera, kan man utan att bryta den eller slå nya hål forma om den till en donits. Med andra ord är kaffemuggen en torus, en sluten kropp med ett hål. Det visar sig att uppgiften är lösbar på en torus, men inte på ett klot eller ett papper!

 

Muggproblemet kan förvånansvärt nog ge oss insikt om ett helt annat problem: Om du har en karta där varje land är en sammanhängande region, hur många färger behöver du för att färglägga varje land utan att två grannländer får samma färg? Då kartan är ritad på ett papper eller en boll visar det sig att högst fyra färger behövs; resultatet är känt som Four color theorem.

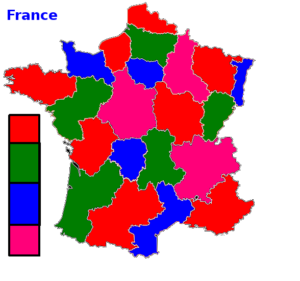
Kartan över Frankrikes provinser behöver fyra färger

Men om kartan är ritad på en annan slags kropp, t.ex. en torus, räcker fyra färger till? För att förstå denna situation bättre söker vi ett ”renare” sätt att rita vår karta. Vi ersätter först varje region med en punkt. Sedan ritar vi streck mellan två punkter ifall de motsvarande regionerna gränsar till varandra. Det vi får är en graf: en samling noder (punkter) och kanter (streck) mellan dessa. I själva verket är det en planär graf, dvs. den kan ritas utan att två streck korsar varandra.

En karta och dess motsvarande graf

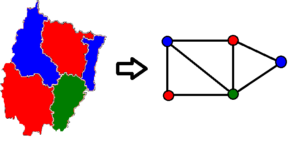
Det visar sig att varje karta motsvarar en planär graf och vice versa. Så istället för att granska kartor på en torus, kan vi kolla på planära grafer på en torus: Hur många färger behövs för att färglägga noderna så att två grannar inte får samma färg? Men här kommer insikten från muggproblemet in: Grafen som bildas i Three Utilities Problem är inte planär på ett papper (dvs två kanter måste korsa varandra) men den är planär på en torus. Det betyder att mängden av planära grafer på en torus är fundamentalt större!

Kan vi alltså hitta en graf som kräver mer än fyra färger? Grafen i muggproblemet kan färgas med endast två färger. Men t.ex. den kompletta grafen K5 kräver 5 färger och kan ritas på en kaffemugg utan att två kanter korsar varandra.

K5 ritad på en kaffemugg utan att två kanter korsar

Och vad är det högsta antalet färger vi kan behöva?
https://mathsgear.co.uk/products/7-colour-torus-mug

Det mest spännande inom matematiken är då två koncept som verkar mycket annorlunda egentligen är nära sammankopplade. Många situationer där vi beaktar föremål (länder) och förbindelser mellan dem (gränser) kan uttryckas med hjälp av grafteori. Men en grafs egenskaper hänger inte bara på grafen själv, utan också på kroppen den ritas på. Kaffemuggen är ett intressant topologiskt föremål, inte bara en pryl för att hälla i sig kaffe.

2018, Vecktraklet

En kollision av rytmer

Lämna en kommentar

Hejssan!

Palles musikhörna är tillbaka med sin naturvetenskapligt inspirerade musik. Och vad tror ni är den vanligaste genren som folk gör låtar i då de försöker göra sitt vetenskapliga ämne coolt?

You guessed it, RAP!

Personligen är jag inget desto större fan av rapmusik, och låtar som denna får mig närmast att vilja krypa ner i ett hål om det behandlar ett ämne jag själv är mer insatt i. Å andra sidan, vad skulle man inte göra för att föra fram sin stora passion? Kan också tänka mig att de som gjort låten haft urkul vid produktionen, så det är inget fel med det heller.

Låten och videon är framställd av flera grupper som haft arbete eller intresse för CERN. Kolla in dem om LHC är din grej!

-Palle

2018, Vecktraklet

Dessa pünschen-prestationer måste tas förr eller senare!

Lämna en kommentar

För ett par veckor sedan diskuterade jag och några äldre spektrumiter om pünschen sådär i förbifarten. Någon nämnde mitt tidigare inlägg om att inte ta pünschen på en dejt och tyckte att detta egentligen skulle vara en minnesvärd och fin pünschenupplevelse. Därför listar jag nu upp fyra tillfällen/platser där det definitivt borde tas en pünschen.

1. I slutet av ett maraton. Detta har jag faktiskt funderat på att skulle vara helt supernajs (och väldigt konstigt för alla åskådare). Detta kräver dock att du och din pünschenpartner båda springer maraton lika snabbt. Men, tänk dig efter 42 km löpande kommer någon inhoppande med pünschenbordet på målrakan och ni tar en officiell pünschen sådär helt casually och sedan springer båda de resterande 195 metrarna till mål och ni känner er som äkta vinnare!

2. I bakgrunden av en filmscen. Tänk dig att du tittar på någon film på TV eller bio, och plötsligt märker du att någon i bakgrunden håller på att ta en pünschen. Jag vet inte i vilken film detta skulle pass in i, men åtminstone skulle resten av världen få ta del av vårt glädjebudskap 🙂 Alternativt skulle detta kunna hända i bakgrunden av en nyhetssändning.

3. Spektrum 100 år och 100 pünschen-evenemanget. När Spektrum om knappa 15 år fyller 100 år borde det ordnas ett evenemang där man försöker ta 100 pünschen samtidigt (ett världsrekord som Spektrum skulle kunna vara stolt över). Detta skulle kräva 200 hävare, 200 domare, ett stort torg (typ Senatstorget nära Klubben?), 35 liter punsch och en aning planerande, men gemenskapen och fiilisen efteråt torde vara fenomenal.

4. På altaret under sin egen vigsel. Finns det månne ett bättre sätt att fira en kärleksfull dag än detta. Bröllop är ju ändå en fest för att fira brudparet och då tycker jag att när man har bestämmanderätt över saker som detta, så skall man få göra det man vill! Kan dock vara lite svårt att hitta en präst som går med på detta (knappast mycket lättare på magistraten heller…), men ifall man utbildar prästen att vara domare kanske det lyckas. En ganska ultimat spektral pünschenprestation åtminstone enligt mig.

_Frans