Matematiska texter från antikens och medelålderns Indien hade en egendomlig struktur. För att hjälpa läsaren minnas dem framställdes problem och resultat ofta som vers. Till exempel Bakshali-manuskriptet är en sådan text.
I nutidens utbildning är poesi en form som används väldigt lite inom vetenskaplig utbildning. Trots det hittar man på nätet många matematiska verser, som människor skrivit för skojs skull eller för att minnas dem bättre. En särskilt minnesvärd versform är limericken, varav några presenteras till näst (i ökande svårighetsgrad):
”A dozen, a gross and a score
Plus three times the square root of four
Divided by seven
Plus five times eleven
Is nine squared and not a bit more”
Ramsan beskriver följande simpla uträkning:
Huruvida ramsan är användbar eller inte lämnas till läsarens beaktande. Till näst nåt en aning knepigare:
”The integral z squared dz
From one to the cube root of three
Times the cosine
Of three pi over nine
Is the log of the cube root of e”
Här beskrivs en annan identitet:
![\displaystyle\int_{1}^{\sqrt[3]{3}}z^2dz \cdotp \cos{\left(\frac{3\pi}{9}\right)} = \ln{\left(\sqrt[3]{e}\right)}](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cint_%7B1%7D%5E%7B%5Csqrt%5B3%5D%7B3%7D%7Dz%5E2dz+%5Ccdotp+%5Ccos%7B%5Cleft%28%5Cfrac%7B3%5Cpi%7D%7B9%7D%5Cright%29%7D+%3D+%5Cln%7B%5Cleft%28%5Csqrt%5B3%5D%7Be%7D%5Cright%29%7D&bg=ffffff&fg=000000&s=0 "\displaystyle\int_{1}^{\sqrt[3]{3}}z^2dz \cdotp \cos{\left(\frac{3\pi}{9}\right)} = \ln{\left(\sqrt[3]{e}\right)}")
Läsaren må påminnas att 
![\ln{\left(\sqrt[3]{e}\right)} = \frac{1}{3}](http://s0.wp.com/latex.php?latex=%5Cln%7B%5Cleft%28%5Csqrt%5B3%5D%7Be%7D%5Cright%29%7D+%3D+%5Cfrac%7B1%7D%7B3%7D&bg=ffffff&fg=000000&s=0 "\ln{\left(\sqrt[3]{e}\right)} = \frac{1}{3}")
I allmänhet är de två föregående verserna skrivna mer för poesins skull, inte för innehållet. Till sist ett mer sofistikerat resultat:
”Take M a complete metric space
If nonempty, it’s always the case
That if f’s a contraction
Then under its action
Exactly one point stays in place”
Versen beskriver den s.k. Banachs fixpunktssatsen. Utan att överkomplicera: I ett fullständigt metriskt rum gäller att om på varandra följande punkter i en följd kommer godtyckligt nära varandra, så har också hela följden en gränspunkt den går mot. En kontraktion är en funktion som, givet två godtyckliga punkter, flyttar dem närmare varandra än de var förut.
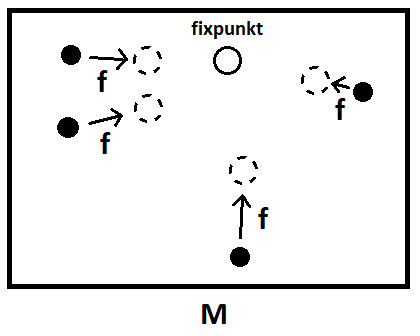
Satsen säger, att kontraktionen f har endast en unik fixpunkt, dvs. en punkt som inte rör sig då kontraktionen appliceras.
Limericken om Banachs fixpunktssats hjälpte mig faktiskt minnas satsen till provet i topologi. Poesi är ett kraftigt verktyg för att få något att fastna i huvudet, och jag skulle vilja se det användas oftare inom matematikutbildningen. Så länge innehållet är ändamålsenligt alltså; förvränger man ekvationer för att göra dem till limericks så gör man det nog mest för poesins skull.
