Mycket av det som görs i Gumtäkt och speciellt i Exactum handlar om någon form av problemlösning. Redan under grundkursen i Analys presenteras man varje vecka med åtminstone sex problem man förväntas kunna lösa. Problemen förföljer studerandena genom hela kandidat-, magisterexamen och för vissa även in i forskningsvärlden. Ofta kritiseras dessa problem; jag är nästan säker på att så gott som alla som studerat matematik eller data har i något skede av studierna tyckt att problemen som skall lösas är helt för artificiella, eller abstrakta för att vara intressanta: vem bryr sig om varför man inte får dela med ? För att hålla kvar de få matematikstuderanden vi har tänkte jag i denna text dela med mig ett exempel av applicering av abstrakta problemlösningstekniker för att åstadkomma saker som på riktigt spelar någon roll. Som huvudpersoner i historien fungerar tre namnlösa spektrumiter som vi kallar för Lasse, Peter och Jeremias, alla med en matematisk/datavetenskaplig utbildning.
Varje problemlösning börjar med ett problem. I vårt fall började vi från följande scenario:
Tänk dig att du och två av dina vänner vid en given tidpunkt har fått en lapp med gåtor vars lösningar är sex olika barer i Helsingfors. Er uppgift är, att snabbare än 200 andra grupper på 3 människor, ta er till alla av dessa sex barer, inmundiga 1.5l öl på varje ställe, sedan ta er till Otnäs och inmundiga 1.5l öl till. Som färdmedel får endast allmäntransport användas.” För enkelhetens skull kommer jag från och med nu kalla detta scenario för ”Problem Y”.
Problemlösning i sig är ett forskningsområde inom kognitiv psykologin. Inte oväntat så verkar det inte finnas ett absolut svar på frågan ”hur skall man göra för att lösa problem?”. Det finns dock vissa standardtekniker för problemlösning som dyker upp i olika undersökningar. Den man ofta börjar med inom matematik och datavetenskap kallas abstraktion. Abstraktion går ut på att exakt definiera vad man försöker åstadkomma, samt identifiera vilka delar av den information man har som behövs för att utveckla en lösning. Dessutom brukar man under abstraktion ofta identifiera begränsningar som sätts på de metoder man kan använda i sin lösning. Ett sätt att beskriva problemet efter abstraktion är genom att använda orden ”INPUT” för att beskriva den (viktiga) informationen man har, ”OBJECTIVE” för att beskriva det man försöker åstadkomma och ”CONSTRAINTS” för att beskriva de begränsningar ens lösning måste följa. Då det kommer till problem Y lyckades vi inte komma på ett sätt att använda (lagliga) datavetenskapliga/matematiska metoder för att hjälpa oss med inmundigandet av liter vätska eller påverka de
andra lagen. Därför bestämde vi oss för att ignorera dessa delar av Y och fokusera på lösningen av gåtorna samt bestämmandet av rutten att ta. Som begränsningar för problemet identifierade vi faktumet att rutten måste endast bestå av allmäntransport. Efter abstraktion såg Y alltså ut såhär:
INPUT: startställe, gåtor till 6 barer
OBJECTIVE: Kortast möjligast tid för att lösa gåtorna, ta sig runt till barerna och sedan ta sig till Otnäs.
CONSTRAINTS: Endast allmänna färdmedel tillåtna.
 Intressant nog betyder abstraktion inom konst oftast inte ”göra saker klarare”.
Intressant nog betyder abstraktion inom konst oftast inte ”göra saker klarare”.
Efter abstraktion är det sedan dags att börja söka en lösning. En inom psykologin identifierad och inom Exactum utlärd teknik för problemlösning kallas divide and conquer. Idén är att spjälka upp ett komplext problem i mindre delar i hopp om att delarna skall vara lättare att lösa. Ofta strävar man till att delproblemen är oberoende av varandra, då kan nämligen alla delproblem lösas samtidigt. I bästa fall kan optimala lösningarna av delproblemen sen kombineras för att åstadkomma en optimal lösning på ursprungliga problemet. Det finns ett ganska naturligt sätt att dela in Y: lösningen av gåtorna samt bestämmande av rutten. Visserligen är dessa två problem inte riktigt oberoende, man kan inte bestämma rutten innan man har löst alla barer. Vi bestämde oss ändå för att dela in Y såhär i hopp om att gåtlösaren skulle bli tillräckligt effektiv för oss att ha någon nytta av rutlösaren. Olyckligt nog visade det sig att gåtlösning högst troligen är för svårt för oss att automatisera. Det finns en dator vid namnet Watson som har lyckats slå de bästa människorna på Jeopardy, men att åstadkomma detta tog 7 år för IBM:s topp ingenjörer. För att vara effektiv måste Watson dessutom köras parallellt på 70 datorer samtidigt. Eftersom vi inte kände för att börja bära omkring på 70 datorer samt inte hade 7 år att sätta på projektet, var det bästa vi kunde hoppas på ett hjälpmedel för gåtlösning, inte en automatisering. Det vill säga, vi skulle inte kunna kombinera lösningarna av delproblemen för att få en optimal lösare av Y. Liknande fenomen sker ofta inom datavetenskap/matematik. Ifall ursprungliga problemet man löser är ”tillräkligt svårt” kan man inte kombinera dellösningarna för att åstadkomma en optimal lösning. Men ofta visar det sig att den (lite sämre) lösningen man åstadkommer ändå är ”tillräkligt bra”, vilket också kommer att vara fallet med Y. Resten av denna text kommer att koncentrera sig på rutt-lösnings problemet: ”givet 6 barer samt en startposition hitta snabbaste sättet att ta sig till alla 6 barer och Otnäs med hjälp av allmäntransport”. Detaljerna av gåtlösaren kommer eventuellt att publiceras i ett senare skede (läs: ifall jag inte får en bättre idé för en höstartikel).
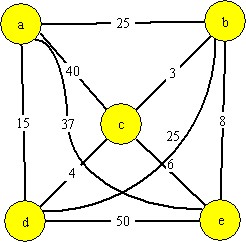
Då man söker efter en lösning till ett ovanligare problem är det alltid inte klart att det man försöker göra är svårt. Detta kan vara bra att ta reda på; det är rätt så onödigt att utveckla hemskt komplicerade lösningar till problem som egentligen (bevisligen) är simpla. ”Hur svårt kan det vara?” var alltså nästa fråga vi ställde oss. En systematisk analys av olika problems svårighet är ett delområde inom komplexitetsteori och är ett forskningsområde för sig. Tekniska detaljer åsido så går analyserna av problemsvårigheter ofta ut på att man förliknar sitt problem med andra kända problem som man vet är svåra/lätta. Ofta är dessa kända problem relativt abstrakta, mest p.g.a. att det skall vara enklare att se likheterna mellan dem och det egna problemet. Då det kommer till vårt problem: ”givet en start position, 6 barer samt ett mål, hitta snabbaste rutten till alla” finns det ett relativt känt problem som man enkelt kan jämföra med, nämligen traveling salesman problem (TSP). I ursprungliga formuleringen av TSP ingår en försäljare som skall besöka alla städer i Tyskland och/eller Schweiz (ursprunget är oklart) i hopp om att sälja sina varor i var och en. Uppgiften är att försöka hitta den kortaste möjliga rutten att göra detta. I en mer abstrakt formulering av TSP har man en matematisk graf bestående av något antal noder och kanter där varje kant har en given längd. Målet är att hitta den kortaste möjliga rutten genom grafen som besöker varje nod åtminstone en gång. Ruttlösningen för problem Y kan ses som travelling salesman där noderna i grafen är de 8:a olika platserna som skall besökas och längden på en kant mellan två noder är tiden som det tar att ta sig mellan dem med allmäntransport. Denna jämförelse mellan problemen är tillräcklig för vårt behov, men inte helt fullständig, vilket vi kommer att märka lite senare.
Efter att man ”känt igen” sitt problem kan man sen dra slutsatser på huruvida man kan förvänta sig att det går att komma fram till en lösning som fungerar inom en rimlig tid. I vårt fall skulle ju en rutt-lösare inte hjälpa hemskt mycket ifall det skulle ta 5 timmar att använda den. Olyckligt nog är traveling salesman ett NP-svårt problem. Igen tekniska detaljer åsido, betyder detta att det i allmänna fallet knappast finns ett effektivt sätt att lösa TSP. Tur i oturen kommer dessa teoretiska begränsningar emot endast då man ökar mängden noder i grafen. Med andra ord så går det troligtvis inte att koda en effektiv ruttlösare för att komma till 100 barer. Men detta var ju inte vad vi var ute efter; våra levrar skulle ändå inte stå ut med så mycket öl. Att lösa rutten till 6 barer borde däremot inte vara en utmaning, ens åt Lasses miniläppäre. Vi kunde alltså fortsätta på projektet trots vissa teoretiska begränsningar.
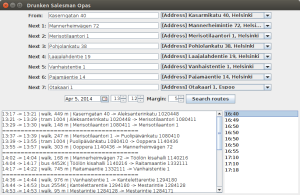
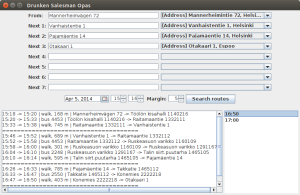
Efter all förberedning visade sig själva kodandet av ruttlösaren var relativt lätt. Efter lite undersökning märkte vi nämligen att HSL bjuder på ett gratis gränssnitt till sin reittiopas, vilket i princip betyder att programmerandet av en normal reittiopas skulle (nästan) kunna vara en uppgift under ohjelmoinnin jatkokurssi. Inspirerade av detta samt de tidigare teoretiska funderingarna döpte vi vår ruttlösare till Drunken Salesman Opas (DSOPAS). Under kodandet av DSOPAS stötte vi egentligen endast på ett till problem som förhindrade oss från att lösa rutten optimalt. Problemet har att göra med jämförelsen av vårt problem och TSP. Då det kommer till allmän transportation kan det ju nämligen hända att tiden det tar att komma från bar X till Y är olika beroende på vilken tid på dagen man reser. Mera matematiskt formulerat så är längden av varje kant i grafen inte konstant. Detta betyder att för en optimal lösning av vårt problem borde reittiopas ”frågas” skilt för vikten av alla kanter i varje rutt möjlighet som undersöks. I en rutt ingår kanter, allt som allt finns det
olika ruttmöjligheter. Totalt skulle algoritmen vid varje körning vara tvungen att fråga reittiopas efter längden av
kanter. Detta skulle annars inte vara ett problem, men HSL tillåter endast
frågor i timmen. Så fast det skulle vara helt möjligt att koda DSOPAS såhär, skulle det ta minst en timme att köra den. För att komma över detta problem bestämde vi oss för att än en gång approximera optimala lösningen genom att helt enkelt skita i att tiderna eventuellt ändrar. Den slutgiltiga DSOPAS börjar alltså med att fråga reittiopas efter tiden det tar att röra sig mellan alla 8 platser (6 barer, start och mål) vid en fixerad tidpunkt (
kanter mellan barerna,
från startpunkten till de olika barerna och
från de olika barerna till målet, allt som allt
). Efter det löser DSOPAS den kortaste rutten i denna ”approximeringsgraf” med hjälp av en sofistikerad algoritm känd som ”prova alla möjligheter”. Under lösningen behöver DSOPAS inte fråga reittiopas alls. Slutligen väljer DSOPAS ut de 5 snabbaste rutterna, vilka sen körs på nytt genom reittiopas för att få egentliga tiderna det tar att använda var och en. Dessa fem rutter visas sen åt användaren. Att fråga reittiopas om tiderna för en fixerad rutt kräver ju alltså
frågor. Allt som allt
frågor, betydligt bättre än ursprungliga
.
Näst borde vi kanske anlita en grafisk designer…
Efter att man löst sitt problem så återstår ett sista steg: verifikation av lösningen. Fastän vi kunde testa DSOPAS på påhittade rutter, var vi tvungna att vänta på årets Ylonz (som de flesta av er säkert har fattat är det Ylonz detta handlar om) innan vi kunde veta hur bra det skulle fungera på riktigt. (För att vara helt ärlig blev väntandet inte hemskt långt, sista buggarna i DSOPAS fixades onsdagen innan Ylonz lördagen). Jag kommer inte att prata så hemskt mycket om hur det gick, många av er vet det redan och för resten kan ju nämnas att vårt lag hette ”<script>alert (‘TechSupported’);</script>” samt att resultaten finns här. Jag påstår inte att DSOPAS var ända orsaken till att resultaten ser ut som de gör, men jag kan med största säkerhet säga att den tillsammans med vårt gåtverktyg nog hjälpte betydligt.
Det fanns en bar i årets Ylonz rutt som fungerar väl som exempel för nyttan vi hade av båda verktygen: Park hotell. Då vi, baserat på bilden av ett monopolhotell, slog in ”hotell” i gåtlösaren var ”Park hotell” det enda alternativet vi fick ut. Dumma som vi var trodde vi inte på vårt eget program, men fortsatte istället fundera. Fem minuter senare hade vi löst resten av tipset och kom fram till att gåtlösaren hade rätt från början. Senare, då vi kom fram till baren, visade sig att den långa kön skulle förhindra oss från att hinna på den bussen som DSOPAS hade bestämt åt oss tidigare. Då, detta under tidigare år skulle ha lett till en massa spekulationer på vad vi borde göra näst, kunde vi nu helt enkelt mata in de återstående barerna i DSOPAS på nytt. Den nya rutten vi fick av vårt program visade sig sist och slutligen vara lika snabb som den första vi hade fått.
Den här texten har egentligen två syften. Den ena är ett exempel på hur ”viktiga problem” kan modeleras och lösas genom abstrakta vetenskapliga metoder. Den andra kan sammanfattas i form av en utmaning. Åtminstone 1/3 av laget TechSupported kommer inom snarast framtid att försvinna utomlands och det verkar som vi inte kommer att ha möjlighet att tävla i Ylonz med samma laguppsättning igen. Men det är inget i användningen av DSOPAS samt gåtlösaren som specifikt kräver att man kan programmera. Dvs. om det är något annat Spektrum lag som känner sig intresserade av att pröva hur långt man kommer i Ylonz med lite teknikhjälp är det bara att ta kontakt. Som sagt påstår vi inte att programmen automatiskt leder till framgång, men får man tipsen löst snabbt och är färdig att springa, har man alla möjligheter att klara sig mycket väl. Spektrum har en fin vana att klara sig väl i Ylonz, en vana som började länge före oss. Vad tycker ni, nog skall vi väl hålla segern inom Spektrum några år till?
Jeremias
KÄLLOR:
http://en.wikipedia.org/wiki/Problem_solving
http://en.wikipedia.org/wiki/Watson_%28computer%29
http://mathworld.wolfram.com/TravelingSalesmanProblem.html
http://mathworld.wolfram.com/NP-HardProblem.html
http://staff.science.uva.nl/~ulle/teaching/comsoc/2012/slides/comsoc-complexity-tutorial.pdf