Inledning

Då jag lär mig nya sporter vill jag ofta betrakta dem ur ett matematiskt perspektiv. Darts är en gren som får mig att fundera på allt från algebra till spelteori, och därför vill jag ge en introduktion till hur man kan se på olika sporter och spel. Detta är främst en introduktion till spelformen 501, som är den absolut vanligaste spelformen när det gäller olika dartgrenar. I 501 startar man på 501 poäng varefter man ”kastar bort” poäng tills man når exakt 0. I artikeln kommer ”enheten” p att lämnas bort då man syftar på poäng.

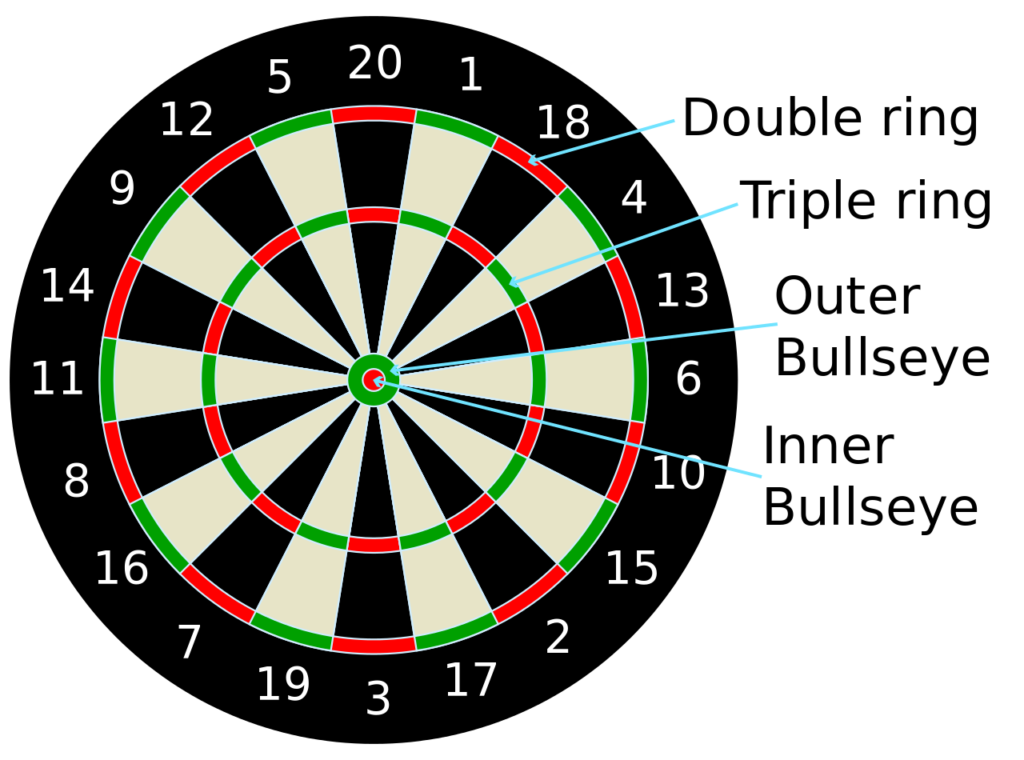
Tavlan

Vi börjar med att gå genom några grundläggande saker då det gäller tavlan och poängräkning. Tavlan placeras så att bullen (mitten av tavlan) ligger på höjden 173 cm. På golvet markeras ett avstånd på 237 cm bakom vilket man måste kasta sina pilar. Tavlan är indelad i 20 lika stora numrerade sektorer (se bilden) som bestämmer hur många poäng sektorn är värd. Den yttersta ringen (dubbelringen) dubblar sektorns poäng och den inre ringen (trippelringen) ger tre gånger sektorns poäng. Exempelvis ett kast i trippelringen på sektor 8 ger 24. I mitten av tavlan finns bullen. Den består av den enkla bullen (gröna ringen) som ger 25 och den dubbla bullen (röda bollen) som ger 50.

501

501-matcher spelas en mot en. Man börjar alltså på 501 och spelar turer tills man når exakt 0. Dessutom måste man ”dubbla ut”, dvs. man måste nå 0 genom att kasta i dubbelringen. En tur går ut på att spelaren kastar tre pilar. Den spelare som först når 0, oberoende vem som börjar, vinner ett så kallat leg. Då man vunnit ett visst antal leg vinner man ett set, och efter ett visst antal vunna set vinner man matchen. Dessa antal beror på turneringen.

Beteckningar

Nästa steg i att börja studera 501 mera matematiskt är att definiera några olika beteckningar. Om vi betecknar en tur som t kan vi exempelvis skriva
,
vilket skulle betyda att spelaren under sin andra tur kastade enkel 7, enkel 19 och trippel 7. Ett kast i dubbelringen betecknas med D.
Eftersom vi främst är intresserade av hur ett helt leg framskrider har vi orsak att nu ännu beteckna spelarens samtliga turer som
.
Vi kan ännu beteckna spelarens totala poäng under ett leg som p(L). Om så vann spelaren alltså ett leg.

Sats: Det krävs åtminstone 9 pilar för att avsluta ett leg.
Bevis: Vi gör ett motantagande, dvs. vi antar att det är möjligt att kasta 501 med 8 pilar eller färre, och samtidigt dubbla ut. För medelvärdet M av kasten gäller alltså nu att
.
Eftersom vilket är det maximala poängantalet för ett kast, så har vi en motsägelse.

Följdsats: Det minsta antal pilar som krävs för att avsluta ett leg är 9.
Bevis: Låt . Då är . Av detta exempel och på basen av föregående sats så är påståendet bevisat.
Ett leg som avslutats efter 9 pilar har fått namnet 9-darter eftersom de är rätt sällsynta. Exemplet ovan är den mest typiska 9-darter eftersom de professionella spelarna vanligtvis siktar på T20.S